题目内容
函数y=
的定义域是 ．
(
|
考点：函数的定义域及其求法
专题：函数的性质及应用
分析：根据函数成立的条件，即可求出函数的定义域．
解答：
解：要使函数f（x）有意义，则(
)x-4≥0，
即2-x≥4，
解得-x≥2，
解得x≤-2，
即函数定义域为（-∞，-2]；
故答案为：（-∞，-2]；
| 1 |
| 2 |
即2-x≥4，
解得-x≥2，
解得x≤-2，
即函数定义域为（-∞，-2]；
故答案为：（-∞，-2]；
点评：本题主要考查函数的定义域的求解，要求熟练掌握常见函数成立的条件．
练习册系列答案
相关题目
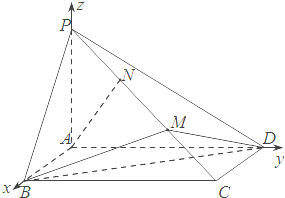己知四棱锥P-ABCD，其中底面ABCD为矩形侧棱PA⊥底面ABCD，其中BC=2，AB=2PA=6，M，N为侧棱PC上的两个三等分点，如图所示：若复数z满足z（1+i）=2i，则复数z等于（ ）
| A、1+i | ||
| B、1-i | ||
C、2+
| ||
| D、2 |