Question

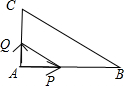在△ABC中，∠B=30°，∠C=60°，AC=1，动点P，Q同时从A出发，沿周界运动，点P沿A→B→C；动点Q沿A→C→B运动到相遇时停止，动点Q的速度是动点P的运动速度的3倍，AP=x，△APQ的面积为y，求函数y=f（x）的解析式，并确定PQ在什么位置时S最大．

Answer 1

考点：根据实际问题选择函数类型

专题：计算题,阅读型

分析：先根据点Q的位置进行分类讨论，然后分别求出三角形的面积，从而可得函数f（x）的解析式，再分别求出面积的最值，从而求出PQ在什么位置时S最大．

解答： 解：因为AP=x，动点Q的速度是动点P的运动速度的3倍，
所以AQ=3x，当点Q在线段AC上时，0＜x≤

1

3

时，三角形APQ为直角三角形，S=

1

2

x•3x=

3

2

x2；
当点Q在线段CB上时，

1

3

＜x≤1时，作出示意图如下：

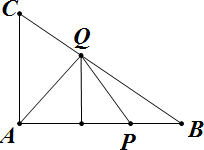
△APQ的高为

BQ

BC

×AC=

3-3x

2

×1=

3-3x

2

，
所以S=

1

2

x•

3-3x

2

=

3x-3x2

4

；
当Q在线段AB上时，不能构成三角形，
所以函数f（x）=

3 2 x2，0＜x≤ 1 3 3x-3x2 4 ， 1 3 ＜x≤1

．
当x=

1

3

时，函数f（x）=

3

2

x2取最大值

1

6

，
当x=

1

2

时，函数f（x）=

3x-3x2

4

取最大值

3

16

．
当点P在AB的中点，Q在BC上，CQ=

1

2

时，f（x）取最大值．

点评：本题主要考查了分段函数的应用，以及函数最值的求解，同时考查了学生分析问题和解决问题的能力，以及运算求解的能力．