题目内容
当x∈(0,2]时,函数f(x)=ax2+4(a+1)x-3在x=2处取得最大值,则a的取值范围是( )
A、-
| ||
B、a≥-
| ||
C、-
| ||
| D、a∈R |
考点:二次函数的性质
专题:计算题,函数的性质及应用
分析:分a>0,a=0,a<0三种情况进行讨论,然后根据x的范围结合图象进行求解.
解答:
解:当a=0时,
f(x)=4x-3,x=2时候取得最大值,符合题意;
当a≠0时,对称轴为x=-
,
(1)当a>0时,
要使x=2时候取得最大值,则-
≤1,解得a>0.
(2)当a<0时,要使x=2时候取得最大值,则-
≥2,a≥-
,∴-
≤a<0.
综上所述,a≥-
.
故选B.
f(x)=4x-3,x=2时候取得最大值,符合题意;
当a≠0时,对称轴为x=-
| 2+2a |
| a |
(1)当a>0时,
要使x=2时候取得最大值,则-
| 2+2a |
| a |
(2)当a<0时,要使x=2时候取得最大值,则-
| 2+2a |
| a |
| 1 |
| 2 |
| 1 |
| 2 |
综上所述,a≥-
| 1 |
| 2 |
故选B.
点评:本题考查二次函数的图象和性质,解题时要注意分类讨论思想的合理运用.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
若复数z满足z(1+i)=2i,则复数z等于( )
| A、1+i | ||
| B、1-i | ||
C、2+
| ||
| D、2 |
已知:A={x|y=2x+1}、B={(x,y)|x+4y=13}.则A∩B=( )
| A、{1,3} | |||||
| B、∅ | |||||
C、{(x,y)|
| |||||
| D、{(1,3)} |
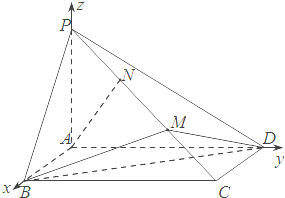 己知四棱锥P-ABCD,其中底面ABCD为矩形侧棱PA⊥底面ABCD,其中BC=2,AB=2PA=6,M,N为侧棱PC上的两个三等分点,如图所示:
己知四棱锥P-ABCD,其中底面ABCD为矩形侧棱PA⊥底面ABCD,其中BC=2,AB=2PA=6,M,N为侧棱PC上的两个三等分点,如图所示: