题目内容
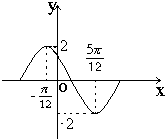 若函数y=Asin(ωx+φ)(ω>0,0<φ<π)在一个周期内的图象如图所示,则
若函数y=Asin(ωx+φ)(ω>0,0<φ<π)在一个周期内的图象如图所示,则(1)写出函数的周期;
(2)求函数的解析式;
(3)求函数的单调增区间.
考点:由y=Asin(ωx+φ)的部分图象确定其解析式,正弦函数的单调性
专题:三角函数的图像与性质
分析:(1)根据函数图象即可写出函数的周期;
(2)根据三角函数的图象和性质,求出A,ω,φ值,即可求函数的解析式;
(3)根据三角函数的单调性之间的关系即可得到结论.
(2)根据三角函数的图象和性质,求出A,ω,φ值,即可求函数的解析式;
(3)根据三角函数的单调性之间的关系即可得到结论.
解答:
解:(1)由已知可得函数y=Asin(ωx+ϕ)的图象经过(-
,2)点和(
,-2)
∴A=2,
=
-(-
)=
,即T=π.
(2)∵T=
=π,∴ω=2,
则函数的解析式可化为y=2sin(2x+ϕ),将(-
,2)代入得,
2sin(-
×2+ϕ)=2,即sin(-
+ϕ)=1,
即-
+φ=
+2kπ,k∈Z,
则φ=
+2kπ,
当k=0时,φ=
,此时y=2sin(2x+
).
(3)由-
+2kπ≤2x+
≤2kπ+
,k∈Z,解得-
+2kπ≤2x≤-
+2kπ,k∈Z,
即-
+kπ≤x≤-
+kπ,k∈Z,
即函数的单调递增区间为[-
+kπ,-
+kπ],k∈Z.
| π |
| 12 |
| 5π |
| 12 |
∴A=2,
| T |
| 2 |
| 5π |
| 12 |
| π |
| 12 |
| π |
| 2 |
(2)∵T=
| 2π |
| ω |
则函数的解析式可化为y=2sin(2x+ϕ),将(-
| π |
| 12 |
2sin(-
| π |
| 12 |
| π |
| 6 |
即-
| π |
| 6 |
| π |
| 2 |
则φ=
| 2π |
| 3 |
当k=0时,φ=
| 2π |
| 3 |
| 2π |
| 3 |
(3)由-
| π |
| 2 |
| 2π |
| 3 |
| π |
| 2 |
| 7π |
| 6 |
| π |
| 6 |
即-
| 7π |
| 12 |
| π |
| 12 |
即函数的单调递增区间为[-
| 7π |
| 12 |
| π |
| 12 |
点评:本题考查的知识点是由函数y=Asin(ωx+ϕ)的部分图象确定其解析式,根据A,ω,φ的关系是解决本题的关键.

练习册系列答案
相关题目
 如图,分别写出适合下列条件的角的集合:
如图,分别写出适合下列条件的角的集合: 如图,已知PA⊥平面ABCD,四边形ABCD是矩形,PA=AB=1,AD=
如图,已知PA⊥平面ABCD,四边形ABCD是矩形,PA=AB=1,AD=