题目内容
已知等差数列{an}不是常数列,a1+a2=4,a2、a5、a14成等比数列.
(Ⅰ)求数列{an}的通项公式.
(Ⅱ)设bn=
,Sn是数列{bn}的前n项,求Sn.
(Ⅰ)求数列{an}的通项公式.
(Ⅱ)设bn=
| 1 |
| anan+1 |
考点:数列的求和,等差数列的通项公式,等差数列的性质
专题:等差数列与等比数列
分析:(Ⅰ)根据等差数列和等比数列的通项公式,建立方程关系即可求数列{an}的通项公式.
(Ⅱ)求出数列{bn}的通项公式,利用裂项法即可得到结论.
(Ⅱ)求出数列{bn}的通项公式,利用裂项法即可得到结论.
解答:
解:(Ⅰ)设等差数列的公差是d,
因数列不是常数列,则d≠0,
∵a2、a5、a14等比,∴
=a2a14,
又a1+a2=4,
∴
,
解这个方程组,得
.
∴an=a1+(n-1)d=1+2(n-1)=2n-1,
即的通项公式为an=2n-1.
(Ⅱ)∵an=2n-1,bn=
,
∴bn=
=
(
-
),
∴Sn=b1+b2+…+bn=
(
-
)+
(
-
)+…+
(
-
)=
(1-
)=
.
因数列不是常数列,则d≠0,
∵a2、a5、a14等比,∴
| a | 2 5 |
又a1+a2=4,
∴
|
解这个方程组,得
|
∴an=a1+(n-1)d=1+2(n-1)=2n-1,
即的通项公式为an=2n-1.
(Ⅱ)∵an=2n-1,bn=
| 1 |
| anan+1 |
∴bn=
| 1 |
| (2n-1)(2n+1) |
| 1 |
| 2 |
| 1 |
| 2n-1 |
| 1 |
| 2n+1 |
∴Sn=b1+b2+…+bn=
| 1 |
| 2 |
| 1 |
| 1 |
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 5 |
| 1 |
| 2 |
| 1 |
| 2n-1 |
| 1 |
| 2n+1 |
| 1 |
| 2 |
| 1 |
| 2n+1 |
| n |
| 2n+1 |
点评:本题主要考查数列的通项公式和数列求和,要求熟练掌握裂项法求和,考查学生的运算能力.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
函数y=x2•cosx的导数为( )
| A、2xcosx+x2sinx |
| B、x2sinx-2xcosx |
| C、2xcosx-x2sinx |
| D、x2cosx-2xsinx |
 函数f(x)=6cos2
函数f(x)=6cos2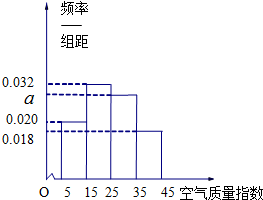 去年2月29日,我国发布了新修订的《环境空气质量标准》指出空气质量指数在0-50为优秀,各类人群可正常活动.惠州市环保局对我市2014年进行为期一年的空气质量监测,得到每天的空气质量指数,从中随机抽取50个作为样本进行分析报告,样本数据分组区间为(5,15],(15,25],(25,35],(35,45],由此得到样本的空气质量指数频率分布直方图,如图.
去年2月29日,我国发布了新修订的《环境空气质量标准》指出空气质量指数在0-50为优秀,各类人群可正常活动.惠州市环保局对我市2014年进行为期一年的空气质量监测,得到每天的空气质量指数,从中随机抽取50个作为样本进行分析报告,样本数据分组区间为(5,15],(15,25],(25,35],(35,45],由此得到样本的空气质量指数频率分布直方图,如图.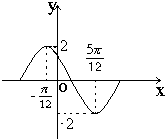 若函数y=Asin(ωx+φ)(ω>0,0<φ<π)在一个周期内的图象如图所示,则
若函数y=Asin(ωx+φ)(ω>0,0<φ<π)在一个周期内的图象如图所示,则