题目内容
正项数列{an}的前n项和Sn满足:Sn2-(n2+n-1)Sn-(n2+n)=0
(1)求数列{an}的通项公式;
(2)令bn=
,求数列{bn}的前n项和Tn.
(1)求数列{an}的通项公式;
(2)令bn=
| an |
| 3n |
考点:数列的求和,数列递推式
专题:等差数列与等比数列
分析:(1)由已知条件推导出Sn>0,Sn=n2+n,由此能推导出数列{an}的通项an=2n.
(2)由bn=
,利用错位相减法能求出Tn=
-
(
)n.
(2)由bn=
| 2n |
| 3n |
| 3 |
| 2 |
| 2n+3 |
| 2 |
| 1 |
| 3 |
解答:
(1)解:由
-(n2+n-1)Sn-(n2+n)=0,
得[Sn-(n2+n)](Sn+1)=0.
∵{an}是正项数列,
∴Sn>0,Sn=n2+n.
∴a1=S1=2,
n≥2时,an=Sn-Sn-1=n2+n-(n-1)2-(n-1)=2n.
综上,数列{an}的通项an=2n.
(2)∵bn=
,∴bn=
,
∴Tn=
+
+
+…+
,①
Tn=
+
+
+…+
,②
①-②,得:
Tn=2(
+
+…+
)-
=2×
-
=1-
-
,
∴Tn=
-
(
)n.
| S | 2 n |
得[Sn-(n2+n)](Sn+1)=0.
∵{an}是正项数列,
∴Sn>0,Sn=n2+n.
∴a1=S1=2,
n≥2时,an=Sn-Sn-1=n2+n-(n-1)2-(n-1)=2n.
综上,数列{an}的通项an=2n.
(2)∵bn=
| an |
| 3n |
| 2n |
| 3n |
∴Tn=
| 2 |
| 3 |
| 4 |
| 32 |
| 6 |
| 33 |
| 2n |
| 3n |
| 1 |
| 3 |
| 2 |
| 32 |
| 4 |
| 33 |
| 6 |
| 34 |
| 2n |
| 3n+1 |
①-②,得:
| 2 |
| 3 |
| 1 |
| 3 |
| 1 |
| 32 |
| 1 |
| 3n |
| 2n |
| 3n+1 |
=2×
| ||||
1-
|
| 2n |
| 3n+1 |
=1-
| 1 |
| 3n |
| 2n |
| 3n+1 |
∴Tn=
| 3 |
| 2 |
| 2n+3 |
| 2 |
| 1 |
| 3 |
点评:本题考查数列的通项公式的求法,考查数列的前n项和的求法,解题时要认真审题,注意错位相减法的合理运用.

练习册系列答案
相关题目
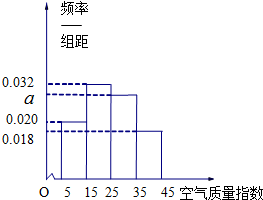 去年2月29日,我国发布了新修订的《环境空气质量标准》指出空气质量指数在0-50为优秀,各类人群可正常活动.惠州市环保局对我市2014年进行为期一年的空气质量监测,得到每天的空气质量指数,从中随机抽取50个作为样本进行分析报告,样本数据分组区间为(5,15],(15,25],(25,35],(35,45],由此得到样本的空气质量指数频率分布直方图,如图.
去年2月29日,我国发布了新修订的《环境空气质量标准》指出空气质量指数在0-50为优秀,各类人群可正常活动.惠州市环保局对我市2014年进行为期一年的空气质量监测,得到每天的空气质量指数,从中随机抽取50个作为样本进行分析报告,样本数据分组区间为(5,15],(15,25],(25,35],(35,45],由此得到样本的空气质量指数频率分布直方图,如图.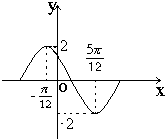 若函数y=Asin(ωx+φ)(ω>0,0<φ<π)在一个周期内的图象如图所示,则
若函数y=Asin(ωx+φ)(ω>0,0<φ<π)在一个周期内的图象如图所示,则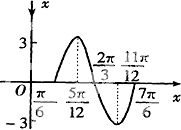 已知函数y=Asin(ωx+φ)(|φ|<
已知函数y=Asin(ωx+φ)(|φ|<