题目内容
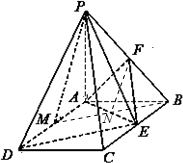
 如图,已知PA⊥平面ABCD,四边形ABCD是矩形,PA=AB=1,AD=
如图,已知PA⊥平面ABCD,四边形ABCD是矩形,PA=AB=1,AD=| 3 |
(Ⅰ)求三棱锥P-ADE的体积;
(Ⅱ)求证:AF⊥平面PBC;
(Ⅲ)若点M为线段AD中点,求证:PM∥平面AEF.
考点:棱柱、棱锥、棱台的体积,直线与平面平行的判定,直线与平面垂直的判定
专题:计算题,空间位置关系与距离
分析:(Ⅰ)PA为三棱锥P-ADE的高,代人三棱锥体积公式计算;(Ⅱ)线面垂直的判定,BC⊥AF,PB⊥AF,∴AF⊥平面PBC;(Ⅲ)线面平行的判定,PM∥FN,∵PM?面AEF,NF?面AEF,∴PM∥平面AEF.
解答:
 (Ⅰ)解:∵PA⊥平面ABCD,
(Ⅰ)解:∵PA⊥平面ABCD,
∴PA为三棱锥P-ADE的高,…2
S△ADE=
×
×1=
,
∴VP-ADE=
×
×1=
,…4
(Ⅱ)证明:∵PA⊥平面ABCD,BC?面ABCD,∴PA⊥BC,
∵AB⊥BC,AB∩PA=A,∴BC⊥面PAB,
∴PM∥FN∵AF?面PAB,∴BC⊥AF,…6
∵PA=AB,F是PB的中点,
∴PB⊥AF,又BC∩PB=B,
∴AF⊥平面PBC;…8
(Ⅲ)证明:连接BM交AE于N,连接PM、FN,
∵四边形ABCD是矩形,∴AD∥BC,且AD=BC,
又M、E分别为AD、BC的中点,∴四边形AMEB是平行四边形,
∴N为BM中点,又∵F是PB的中点,
∴PM∥FN,∵PM?面AEF,NF?面AEF,
∴PM∥平面AEF.
 (Ⅰ)解:∵PA⊥平面ABCD,
(Ⅰ)解:∵PA⊥平面ABCD,∴PA为三棱锥P-ADE的高,…2
S△ADE=
| 1 |
| 2 |
| 3 |
| ||
| 2 |
∴VP-ADE=
| 1 |
| 3 |
| ||
| 2 |
| ||
| 6 |
(Ⅱ)证明:∵PA⊥平面ABCD,BC?面ABCD,∴PA⊥BC,
∵AB⊥BC,AB∩PA=A,∴BC⊥面PAB,
∴PM∥FN∵AF?面PAB,∴BC⊥AF,…6
∵PA=AB,F是PB的中点,
∴PB⊥AF,又BC∩PB=B,
∴AF⊥平面PBC;…8
(Ⅲ)证明:连接BM交AE于N,连接PM、FN,
∵四边形ABCD是矩形,∴AD∥BC,且AD=BC,
又M、E分别为AD、BC的中点,∴四边形AMEB是平行四边形,
∴N为BM中点,又∵F是PB的中点,
∴PM∥FN,∵PM?面AEF,NF?面AEF,
∴PM∥平面AEF.
点评:本题考查棱锥的体积,线面垂直,线面平行,掌握空间线面位置关系的判定及性质是关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
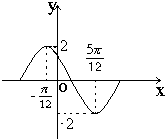 若函数y=Asin(ωx+φ)(ω>0,0<φ<π)在一个周期内的图象如图所示,则
若函数y=Asin(ωx+φ)(ω>0,0<φ<π)在一个周期内的图象如图所示,则