题目内容
已知直线l过两直线x-2y+4=0和x+y-2=0的交点P,求解下列问题:
(1)直线l经过点Q(2,1),求直线l的方程;
(2)直线l与直线3x-4y+5=0平行,求直线l的方程.
(1)直线l经过点Q(2,1),求直线l的方程;
(2)直线l与直线3x-4y+5=0平行,求直线l的方程.
考点:直线的一般式方程与直线的平行关系,直线的一般式方程与直线的垂直关系,两条直线的交点坐标
专题:直线与圆
分析:(1)把直线方程联立可得交点,再利用点斜式即可得出;
(2)根据相互平行的直线斜率之间的关系可设:所求直线方程为:3x-4y+C=0.再把点P代入即可.
(2)根据相互平行的直线斜率之间的关系可设:所求直线方程为:3x-4y+C=0.再把点P代入即可.
解答:
解:(1)由
,解得
,∴P(0,2).
∴kl=
=-
.
故所求直线方程为:y=-
x+2,化为x+2y-4=0.
(2)设所求直线方程为:3x-4y+C=0.
又∵过P(0,2),∴0-4×2+C=0,解得C=8.
∴直线方程为:3x-4y+8=0.
|
|
∴kl=
| 2-1 |
| 0-2 |
| 1 |
| 2 |
故所求直线方程为:y=-
| 1 |
| 2 |
(2)设所求直线方程为:3x-4y+C=0.
又∵过P(0,2),∴0-4×2+C=0,解得C=8.
∴直线方程为:3x-4y+8=0.
点评:本题考查了直线的交点、点斜式、相互平行的直线斜率之间的关系,属于基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
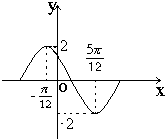 若函数y=Asin(ωx+φ)(ω>0,0<φ<π)在一个周期内的图象如图所示,则
若函数y=Asin(ωx+φ)(ω>0,0<φ<π)在一个周期内的图象如图所示,则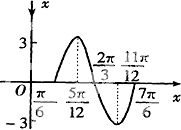 已知函数y=Asin(ωx+φ)(|φ|<
已知函数y=Asin(ωx+φ)(|φ|<