题目内容
已知椭圆P的中心O在坐标原点,焦点在x轴上,且经过点A(0,2
),离心率为
.
(Ⅰ)求椭圆P的方程;
(Ⅱ)是否存在过点E(0,-4)的直线l交椭圆P于点R、T,且满足
•
=8,若存在,求直线l的方程;若不存在,说明理由.
| 3 |
| 1 |
| 2 |
(Ⅰ)求椭圆P的方程;
(Ⅱ)是否存在过点E(0,-4)的直线l交椭圆P于点R、T,且满足
| OR |
| OT |
考点:椭圆的简单性质
专题:综合题,圆锥曲线的定义、性质与方程
分析:(Ⅰ)设椭圆P的方程为
+
=1(a>b>0),由椭圆经过点A(0,2
),离心率为
,求得a和b的值,
从而求得椭圆P的方程.
(Ⅱ)由y=kx-4代入椭圆方程可得x1+x2和x1•x2 的值,可得y1•y2的值,根据
•
=8,求出k,从而得到直线l的方程.
| x2 |
| a2 |
| y2 |
| b2 |
| 3 |
| 1 |
| 2 |
从而求得椭圆P的方程.
(Ⅱ)由y=kx-4代入椭圆方程可得x1+x2和x1•x2 的值,可得y1•y2的值,根据
| OR |
| OT |
解答:
解:(I)设椭圆P的方程
+
=1(a>b>0),由题意得b=2
,
=
,
∴a=2c,b2=a2-c2=3c2,∴c=2,a=4,∴椭圆P的方程为:
+
=1.
(II)假设存在满足题意的直线L.易知当直线的斜率不存在时,
•
<0,不满足题意.
故设直线L的斜率为k,R(x1,y1),T(x2,y2 ).
∵
•
=8,∴x1x2+y1y2=8,
由y=kx-4代入椭圆方程可得(3+4k2 )x2-32kx+16=0,
由△=(-32k)2-4(3+4k2)×16>0,
解得k2>
①.
∴x1+x2=
,x1x2=
,
∴y1y2=(kx1-4 )(kx2-4)=k2 x1•x2-4k(x1+x2)+16,
∴x1x2+y1y2=
-
=8
∴k2=
②,
由①、②解得 k=±
,∴直线l的方程为y=±
x-4,
故存在直线l:y=±
x-4满足题意.
| x2 |
| a2 |
| y2 |
| b2 |
| 3 |
| c |
| a |
| 1 |
| 2 |
∴a=2c,b2=a2-c2=3c2,∴c=2,a=4,∴椭圆P的方程为:
| x2 |
| 16 |
| y2 |
| 12 |
(II)假设存在满足题意的直线L.易知当直线的斜率不存在时,
| OR |
| OT |
故设直线L的斜率为k,R(x1,y1),T(x2,y2 ).
∵
| OR |
| OT |
由y=kx-4代入椭圆方程可得(3+4k2 )x2-32kx+16=0,
由△=(-32k)2-4(3+4k2)×16>0,
解得k2>
| 1 |
| 4 |
∴x1+x2=
| 32k |
| 3+4k2 |
| 16 |
| 3+4k2 |
∴y1y2=(kx1-4 )(kx2-4)=k2 x1•x2-4k(x1+x2)+16,
∴x1x2+y1y2=
| 16 |
| 3+4k2 |
| 48-48k2 |
| 3+4k2 |
∴k2=
| 1 |
| 2 |
由①、②解得 k=±
| ||
| 2 |
| ||
| 2 |
故存在直线l:y=±
| ||
| 2 |
点评:本题考查求椭圆的标准方程的方法,直线和圆锥曲线的位置关系,两个向量的数量积公式,求出x1•x2和y1•y2 的值,是解题的关键.

练习册系列答案
相关题目
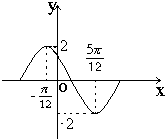 若函数y=Asin(ωx+φ)(ω>0,0<φ<π)在一个周期内的图象如图所示,则
若函数y=Asin(ωx+φ)(ω>0,0<φ<π)在一个周期内的图象如图所示,则 如图,在直三棱柱ABC-A1B1C1中,平面A1BC⊥侧面A1ABB1,且AA1=AB=2.
如图,在直三棱柱ABC-A1B1C1中,平面A1BC⊥侧面A1ABB1,且AA1=AB=2.