题目内容

解不等式：
a2-x2
＞2x-a．
考点：其他不等式的解法
专题：不等式的解法及应用
分析：由原不等式可得
2x-a＜0
a2≥x2
 ①，或
2x-a≥0
a2-x2＞(2x-a)2
②．再分当a=0时、当a＞0时、当a＜0时三种情况，分别求得①和②的解集，综合可得结论．
解答： 解：由不等式
a2-x2
＞2x-a，可得
2x-a＜0
a2≥x2
 ①，或 
2x-a≥0
a2-x2＞(2x-a)2
②．
当a=0时，显然原不等式无解．
当a＞0时，解①求得-a＜x＜
a
2
，解②求得
a
2
≤x＜
4a
5
，故原不等式的解集为（-a，
4a
5
）．
当a＜0时，解①求得 a≤x＜
a
2
，解②求得
a
2
≤x＜0，故原不等式的解集为（a，0）．
点评：本题主要考查根式不等式的解法，体现了转化、分类讨论的数学思想，属于基础题．
练习册系列答案
相关题目
函数f（x）=6cos2
ωx
2
+
3
sinωx-3（ω＞0）在一个周期内的图象如图所示，A为图象的最高点，B、C为图象与x轴的交点，且△ABC为正三角形．
（1）求ω的值及函数f（x）的单调递增区间；
（2）若f（x0）=
8
3
5
，且x0=∈（-
10
3
，
2
3
），求f（x0+1）的值．
已知函数f（x）=x2-2ax+2（a+1）lnx，若函数f（x）有两个极值点，求a的取值范围．
已知α∈（-
π
2
，
π
2
），β∈（0，π），求使等式sin（3π-α）=
2
cos（
π
2
-β），
3
cos（-α）=-
2
cos（π+β）同时成立的角α与β．
设函数f（x）=2ax-
a
x
+lnx
（1）当a=-
1
3
时，若在[
1
4
，2]存在x0，使得不等式f（x0）-c≤0成立，求c的最小值．
（2）若f（x）在（0，+∞）上是单调函数，求a的取值范围．（参考数据e2≈7.389，e3≈20.08）
已知函数f（x）=ax-ex（a＞0）．
（Ⅰ）若a=1，求函数f（x）在[m，m+l]上的最大值；
（Ⅱ）当1≤a≤e+1时，求证：f（x）≤x．
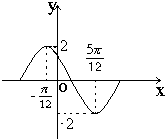若函数y=Asin（ωx+φ）（ω＞0，0＜φ＜π）在一个周期内的图象如图所示，则
（1）写出函数的周期；
（2）求函数的解析式；
（3）求函数的单调增区间．
设函数f（x）=
3
2
cosx+
1
2
sinx+1
（1）求函数f（x）的值域和函数的单调递增区间；
（2）当f（a）=
9
5
，且
π
6
＜α＜
2π
3
时，求sin（2α+
2π
3
）的值．
已知△ABC的面积为4
3
，三个内角A、B、C等差，则
BA
•
BC
=
 
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网