题目内容
某厂生产A,B两型会议桌,每套会议桌需经过加工木材和上油漆两道工序才能完成.已知做一套A,B型会议桌需要加工木材的时间分别为1小时和2小时,上油漆需要的时间分别为3小时和1小时.厂里规定:加工木材的时间每天不得超过8小时,上油漆的时间每天不得超过9小时.已知该厂生产一套A,B型会议桌分别可获得利润2千元和3千元,试问:该厂每天应分别生产A,B两型会议桌多少套,才能获得最大利润?最大利润是多少?
考点:简单线性规划
专题:不等式的解法及应用
分析:设该厂每天应分别生产A,B两型会议桌分别为x,y套,由题意可得
,目标函数z=2x+3y,作可行域平移目标直线易得结论.
|
解答:
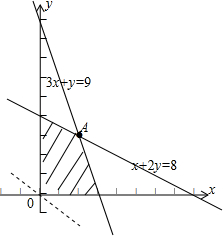 解:设该厂每天应分别生产A,B两型会议桌分别为x,y套,
解:设该厂每天应分别生产A,B两型会议桌分别为x,y套,
由题意可得
,目标函数z=2x+3y,
作出可行域(如图阴影),变形目标函数可得y=-
x+
z
平行直线可知当y=-
x经过点A(2,3)时,z取最大值13,
故该厂每天应分别生产A,B两型会议桌分别为2套,3套时,可或最大利润13000元.
 解:设该厂每天应分别生产A,B两型会议桌分别为x,y套,
解:设该厂每天应分别生产A,B两型会议桌分别为x,y套,由题意可得
|
作出可行域(如图阴影),变形目标函数可得y=-
| 2 |
| 3 |
| 1 |
| 3 |
平行直线可知当y=-
| 2 |
| 3 |
故该厂每天应分别生产A,B两型会议桌分别为2套,3套时,可或最大利润13000元.
点评:本题考查简单线性规划的应用,由实际意义得出约束条件和目标函数并准确作图是解决问题的关键,属中档题.

练习册系列答案
 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案
相关题目
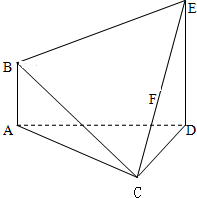 如图所示的多面体ABEDC中,AB⊥平面ACD,DE⊥平面ACD,且AC=CD,DE=2AB=2,AC=CD=7,AD=7,求多面体ABEDC的体积.
如图所示的多面体ABEDC中,AB⊥平面ACD,DE⊥平面ACD,且AC=CD,DE=2AB=2,AC=CD=7,AD=7,求多面体ABEDC的体积.