题目内容
已知函数f（x）=2sin（
+θ）[
sin（
+θ）+cos（
+θ）]，做∠A为△ABC的内角，f（A）=
+1．
（1）求∠A的大小；
（2）若a=3，BC边上的中线长为3，求△ABC的面积．
| π |
| 4 |
| 3 |
| π |
| 4 |
| π |
| 4 |
| 3 |
（1）求∠A的大小；
（2）若a=3，BC边上的中线长为3，求△ABC的面积．
考点：余弦定理,两角和与差的正弦函数
专题：解三角形
分析：（1）把已知由同角三角函数的基本关系式化简，代入f（A）=
+1，结合A的范围求解A的值；
（2）分别在三角形ABC、三角形ADB、三角形ADC中运用余弦定理结合已知条件求得AB•AC的值，代入三角形的面积公式得答案．
| 3 |
（2）分别在三角形ABC、三角形ADB、三角形ADC中运用余弦定理结合已知条件求得AB•AC的值，代入三角形的面积公式得答案．
解答：
解：f（θ）=2sin（
+θ）[
sin（
+θ）+cos（
+θ）]
=2
sin2(
+θ)+2sin(
+θ)cos(
+θ)
=
[1-cos(
+2θ)]+sin(
+2θ)
=
+
sin2θ+cos2θ
=
+2sin(2θ+
)．
（1）由f（A）=
+1，A∈（0，π），得
+2sin(2A+
)=
+1，
sin(2A+
)=
，
∵A∈（0，π），∴A=
；
（2）如图，
在△ABC中，设BC中点为D，∠ADB=α，则∠ADC=π-α，
则BC2=AC2+AB2-2AB•ACcos
，
AB2=AD2+BD2-2AD•BDcosα，
AC2=AD2+DC2-2AD•DCcos（π-α），
又AD=3，BD=DC=
，
联立以上各式求得：AB•AC=
．
∴S△ABC=
AB•ACsin
=
×
×
=
．
解：f（θ）=2sin（| π |
| 4 |
| 3 |
| π |
| 4 |
| π |
| 4 |
=2
| 3 |
| π |
| 4 |
| π |
| 4 |
| π |
| 4 |
=
| 3 |
| π |
| 2 |
| π |
| 2 |
=
| 3 |
| 3 |
=
| 3 |
| π |
| 6 |
（1）由f（A）=
| 3 |
| 3 |
| π |
| 6 |
| 3 |
sin(2A+
| π |
| 6 |
| 1 |
| 2 |
∵A∈（0，π），∴A=
| π |
| 3 |
（2）如图，
在△ABC中，设BC中点为D，∠ADB=α，则∠ADC=π-α，
则BC2=AC2+AB2-2AB•ACcos
| π |
| 3 |
AB2=AD2+BD2-2AD•BDcosα，
AC2=AD2+DC2-2AD•DCcos（π-α），
又AD=3，BD=DC=
| 3 |
| 2 |
联立以上各式求得：AB•AC=
| 45 |
| 2 |
∴S△ABC=
| 1 |
| 2 |
| π |
| 3 |
| 1 |
| 2 |
| 45 |
| 2 |
| ||
| 2 |
45
| ||
| 8 |
点评：本题考查了同角三角函数的基本关系式，考查了余弦定理在解三角形中的应用，考查了学生的计算能力，是中档题．
练习册系列答案
相关题目
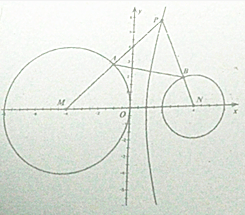已知圆M：x2+8x+y2=0和圆N：x2-8x+y2+12=0，点P（x0，y0）（y0≠0），曲线C：x2-