题目内容
已知数列{an}中,a1=1,an+1=2an+3.求an.
考点:数列递推式
专题:等差数列与等比数列
分析:把数列递推式两边加3得到新数列{an+3},该数列为等比数列,求出其通项公式,则an可求.
解答:
解:由an+1=2an+3,得an+1+3=2(an+3),
∵a1+3=1+3=4≠0,
∴
=2,
∴数列{an+3}是以4为首项,以2为公比的等比数列,
∴an+3=4•2n-1=2n+1,
则an=2n+1-3.
∵a1+3=1+3=4≠0,
∴
| an+1+3 |
| an+3 |
∴数列{an+3}是以4为首项,以2为公比的等比数列,
∴an+3=4•2n-1=2n+1,
则an=2n+1-3.
点评:本题考查了数列递推式,对于an+1=pan+q型的数列递推式,常用构造等比数列的方法求解,是中档题.

练习册系列答案
相关题目
在直角坐标系中,过点A(0,3),B(
,0)的直线l的倾斜角是( )
| 3 |
A、
| ||
B、
| ||
C、
| ||
D、
|
给出四个函数,分别满足①f(x+y)=f(x)+f(y),②g(x+y)=g(x)•g(y),③h(x•y)=h(x)+h(y),④m(x•y)=m(x)•m(y).又给出四个函数的图象,那么正确的匹配方案可以是( )
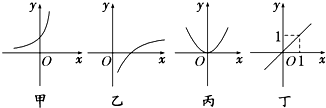

| A、①甲,②乙,③丙,④丁 |
| B、①乙,②丙,③甲,④丁 |
| C、①丙,②甲,③乙,④丁 |
| D、①丁,②甲,③乙,④丙 |
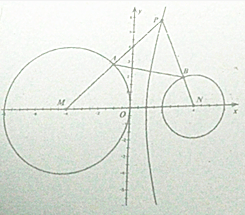 已知圆M:x2+8x+y2=0和圆N:x2-8x+y2+12=0,点P(x0,y0)(y0≠0),曲线C:x2-
已知圆M:x2+8x+y2=0和圆N:x2-8x+y2+12=0,点P(x0,y0)(y0≠0),曲线C:x2-