题目内容
某学校为调查高二年学生的身高情况,按随机抽样的方法抽取80名学生,得到如下的列联表
已知在全部80人中随机抽取一人抽到身高≥170cm的学生的概率是
.
(1)请将上面的列联表补充完整;
(2)能否在犯错误的概率不超过0.001的前提下认为“身高与性别有关”?
(3)在上述80名学生中,身高170~175cm之间的男生有16人,女生人数有4人.
从身高在170~175cm之间的学生中按男、女性别分层抽样的方法,抽出5人,从这5人中选派3人当旗手,求3人中恰好有一名女生的概率.
参考公式:K2=
参考数据:
| ≥170cm | <170cm | 总计 | |
| 男生身高 | 10 | ||
| 女生身高 | 4 | ||
| 总计 | 80 |
| 17 |
| 40 |
(1)请将上面的列联表补充完整;
(2)能否在犯错误的概率不超过0.001的前提下认为“身高与性别有关”?
(3)在上述80名学生中,身高170~175cm之间的男生有16人,女生人数有4人.
从身高在170~175cm之间的学生中按男、女性别分层抽样的方法,抽出5人,从这5人中选派3人当旗手,求3人中恰好有一名女生的概率.
参考公式:K2=
| n(ad-bc)2 |
| (a+b)(c+d)(a+c)(b+d) |
参考数据:
| P(K2≥k0) | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 5.024 | 6.635 | 7.879 | 10.828 |
考点:独立性检验,列举法计算基本事件数及事件发生的概率
专题:概率与统计
分析:(1)根据列联表的组成进行填空;
(2)直接根据K2公式,进行计算;
(3)首先,根据分层抽样进行抽取,然后,按照古典概型公式求解.
(2)直接根据K2公式,进行计算;
(3)首先,根据分层抽样进行抽取,然后,按照古典概型公式求解.
解答:
解:(1)身高≥170cm的人数有80×
=34人,所以可得到下列列联表:
(2)依据K2公式,得
K2=
≈34.58>10.828,…(7分)
∴在犯错误的概率不超过0.001的前提下认为身高与性别有关;…(8分)
(3)在170~175cm之间的男生有16人,女生人数有4人,
按照抽样的方法抽出5人,则男生占4人,女生占1人,
设男生为A1,A2,A3,A4,女生为B,
从5人中任意选3人,有
(A1,A2,A3)、(A2,A1,A4)、(A2,A1,B)
(A3,A1,B)、(A4,A1,B)、(A2,A3,A4)
(A2,A3,B)、(A2,A4,B)、(A3,A4,B)
(A3,A1,A4)
共10种情形,
3人中恰有一名女生的有:
(A2,A1,B)、(A3,A1,B)、(A4,A1,B)
(A2,A3,B)、(A2,A4,B)、(A3,A4,B)
共6种可能,
根据古典概型,得
P=
=
,
∴3人中恰好有一名女生的概率
.
| 17 |
| 40 |
| ≥170cm | <170cm | 总计 | |
| 男生身高 | 30 | 10 | 40 |
| 女生身高 | 4 | 36 | 40 |
| 总计 | 34 | 46 | 80 |
K2=
| 80×(30×36-10×4)2 |
| 40×40×34×46 |
∴在犯错误的概率不超过0.001的前提下认为身高与性别有关;…(8分)
(3)在170~175cm之间的男生有16人,女生人数有4人,
按照抽样的方法抽出5人,则男生占4人,女生占1人,
设男生为A1,A2,A3,A4,女生为B,
从5人中任意选3人,有
(A1,A2,A3)、(A2,A1,A4)、(A2,A1,B)
(A3,A1,B)、(A4,A1,B)、(A2,A3,A4)
(A2,A3,B)、(A2,A4,B)、(A3,A4,B)
(A3,A1,A4)
共10种情形,
3人中恰有一名女生的有:
(A2,A1,B)、(A3,A1,B)、(A4,A1,B)
(A2,A3,B)、(A2,A4,B)、(A3,A4,B)
共6种可能,
根据古典概型,得
P=
| 6 |
| 10 |
| 3 |
| 5 |
∴3人中恰好有一名女生的概率
| 3 |
| 5 |
点评:本题重点考查了K2公式,古典概型等知识,属于中档题.

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案
相关题目
已知{an}是首项为1的等比数列,Sn是{an}的前n项的和,且9S3=S6,则数列{
}的前5项的和为( )
| 1 |
| an |
A、
| ||
B、
| ||
C、
| ||
D、
|
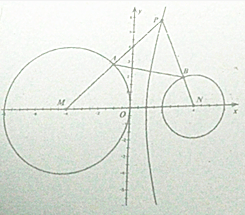 已知圆M:x2+8x+y2=0和圆N:x2-8x+y2+12=0,点P(x0,y0)(y0≠0),曲线C:x2-
已知圆M:x2+8x+y2=0和圆N:x2-8x+y2+12=0,点P(x0,y0)(y0≠0),曲线C:x2-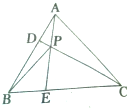 如图所示,正三角形ABC中,D,E分别是AB,BC上的一个三等分点,且分别靠近点A、点B,且AE、CD交于点P.求证:BP⊥DC.
如图所示,正三角形ABC中,D,E分别是AB,BC上的一个三等分点,且分别靠近点A、点B,且AE、CD交于点P.求证:BP⊥DC.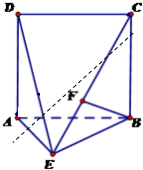 如图,直二面角D-AB-E中,四边形ABCD是边长为2的正方形,AE=EB,F为CE上的点,且BF⊥平面ACE.
如图,直二面角D-AB-E中,四边形ABCD是边长为2的正方形,AE=EB,F为CE上的点,且BF⊥平面ACE.