题目内容
已知A.C是圆O:x2+y2=2上任意两点点A关于x轴的对称点为B,若直线AC,BC分别交x轴于点M(m,0)和N(n,0),则mn= .
考点:关于点、直线对称的圆的方程
专题:直线与圆
分析:不妨设A(0,
)、C(-
,0),则点B(0,-
),由此可得直线AC,BC分别交x轴于点M(m,0)和N(n,0)的坐标,从而求得mn的值.
| 2 |
| 2 |
| 2 |
解答:
解:不妨设A(0,
)、C(-
,0),则点B(0,-
),
则直线AC,BC分别交x轴于点M(-
,0)和N(-
,0),∴mn=-
•(-
)=2,
故答案为:2.
| 2 |
| 2 |
| 2 |
则直线AC,BC分别交x轴于点M(-
| 2 |
| 2 |
| 2 |
| 2 |
故答案为:2.
点评:本题主要考查直线和圆的位置关系,恰当地选择特殊值能够大大地简化运算,属于基础题.

练习册系列答案
相关题目
给出四个函数,分别满足①f(x+y)=f(x)+f(y),②g(x+y)=g(x)•g(y),③h(x•y)=h(x)+h(y),④m(x•y)=m(x)•m(y).又给出四个函数的图象,那么正确的匹配方案可以是( )
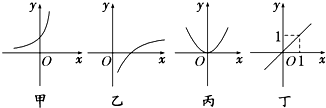

| A、①甲,②乙,③丙,④丁 |
| B、①乙,②丙,③甲,④丁 |
| C、①丙,②甲,③乙,④丁 |
| D、①丁,②甲,③乙,④丙 |