题目内容
已知函数f(x)=x3+1.
(1)求函数f(x)=x3+1在点(1,f(1))处的切线方程;
(2)求该函数的单调区间.
(1)求函数f(x)=x3+1在点(1,f(1))处的切线方程;
(2)求该函数的单调区间.
考点:利用导数研究函数的单调性,利用导数研究曲线上某点切线方程
专题:函数的性质及应用,导数的综合应用
分析:先根据切点在曲线上求出m的值,然后利用导数的几何意义求出在x=1处的导数即为切线的斜率,从而求出切线方程.(2)利用导数的正负,即可求函数f(x)的单调区间.
解答:
解:(1)∵点P(1,f(1))为切点
∴f(1)=2,
∴P (1,2)为切点,
∵y′=3x2
∴y′|x=1=3,切点为(1,2)
∴函数f(x)=x3+1在点(1,2)切线方程为y-2=3(x-1),整理得y=3x-1
所以函数f(x)=x3+1在点(1,f(1))处的切线方程切线方程:3x-y-1=0;
(2)f′(x)=3x2≥0恒成立,
令f′(x)>0,可得x<0或x>1;令f′(x)<0,可得0<x<1,
∴f(x)在定义域内是增函数,单调递增区间是(-∞,+∞).
∴f(1)=2,
∴P (1,2)为切点,
∵y′=3x2
∴y′|x=1=3,切点为(1,2)
∴函数f(x)=x3+1在点(1,2)切线方程为y-2=3(x-1),整理得y=3x-1
所以函数f(x)=x3+1在点(1,f(1))处的切线方程切线方程:3x-y-1=0;
(2)f′(x)=3x2≥0恒成立,
令f′(x)>0,可得x<0或x>1;令f′(x)<0,可得0<x<1,
∴f(x)在定义域内是增函数,单调递增区间是(-∞,+∞).
点评:本题主要考查了利用导数研究曲线上某点切线方程、函数的单调区间,明确导数的几何意义,正确求导是关键.属于基础题.

练习册系列答案
相关题目
给出四个函数,分别满足①f(x+y)=f(x)+f(y),②g(x+y)=g(x)•g(y),③h(x•y)=h(x)+h(y),④m(x•y)=m(x)•m(y).又给出四个函数的图象,那么正确的匹配方案可以是( )
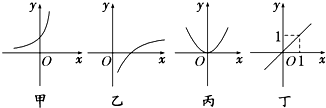

| A、①甲,②乙,③丙,④丁 |
| B、①乙,②丙,③甲,④丁 |
| C、①丙,②甲,③乙,④丁 |
| D、①丁,②甲,③乙,④丙 |
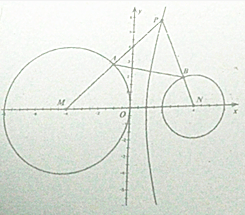 已知圆M:x2+8x+y2=0和圆N:x2-8x+y2+12=0,点P(x0,y0)(y0≠0),曲线C:x2-
已知圆M:x2+8x+y2=0和圆N:x2-8x+y2+12=0,点P(x0,y0)(y0≠0),曲线C:x2-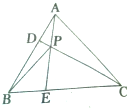 如图所示,正三角形ABC中,D,E分别是AB,BC上的一个三等分点,且分别靠近点A、点B,且AE、CD交于点P.求证:BP⊥DC.
如图所示,正三角形ABC中,D,E分别是AB,BC上的一个三等分点,且分别靠近点A、点B,且AE、CD交于点P.求证:BP⊥DC.