题目内容
参数方程为
(t为参数)的曲线C的普通方程为( )
|
| A、y=-2x+3 |
| B、y=-2x+3(x≥0) |
| C、y=-2x+3(x>1) |
| D、y=-2x+3(x≥1) |
考点:参数方程化成普通方程
专题:坐标系和参数方程
分析:直接消去参数,得到普通方程即可.
解答:
解:∵参数方程为
(t为参数),
∴
=x-1,代入第二个等式,得
y=1-2(x-1)=-2x+3,(x≥1),
即y=-2x+3,(x≥1),
故选:D.
|
∴
| t |
y=1-2(x-1)=-2x+3,(x≥1),
即y=-2x+3,(x≥1),
故选:D.
点评:本题重点考查了直线的普通方程和参数方程的互化等知识,注意参数取值范围,防止范围扩大或缩小.属于基础题,也是易错题.

练习册系列答案
 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案
相关题目
设f(x)为可导函数,且满足
=-1,则函数y=f(x)在x=1处的导数值为( )
| lim |
| △x→0 |
| f(1+△x)-f(1) |
| △x |
| A、1 | B、-1 |
| C、1或-1 | D、以上答案都不对 |
在区间[0,3]上任取一个实数,则此实数小于1的概率为( )
A、
| ||
B、
| ||
C、
| ||
| D、1 |
已知数列{an}为等比数列,a4+a7=2,a5•a6=-8,则a1+a10的值为( )
| A、7 | B、-5 | C、5 | D、-7 |
已知平面上不共线的四点O,A,B,C,若
-4
+3
=0,则
=( )
| OA |
| OB |
| OC |
|
| ||
|
|
| A、3 | B、4 | C、5 | D、6 |
已知函数f(x)=x3+3mx2+nx+m2在x=-1时有极值为0,则m+n=( )
| A、11 | B、4或11 | C、4 | D、8 |
在R上可导的函数f(x)的图形如图所示,则关于x的不等式x•f′(x)<0的解集为( )
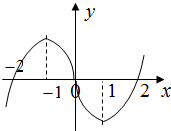
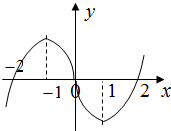
| A、(-∞,-1)∪(0,1) |
| B、(-1,0)∪(1,+∞) |
| C、(-2,-1)∪(1,2) |
| D、(-∞,-2)∪(2,+∞) |
函数y=
sin(2x-
)的图象可以看作是函数y=
sin2x的图象( )
| 1 |
| 2 |
| π |
| 6 |
| 1 |
| 2 |
A、向左平移
| ||
B、向右平移
| ||
C、向左平移
| ||
D、向右平移
|
若f(x)是(-a,a)上的可导奇函数,且f'(x)不恒为零,则f'(x)在(-a,a)上( )
| A、必为奇函数 |
| B、必为偶函数 |
| C、是非奇非偶函数 |
| D、可能为奇函数,也可能是偶函数 |