题目内容
在R上可导的函数f(x)的图形如图所示,则关于x的不等式x•f′(x)<0的解集为( )
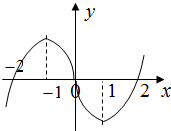
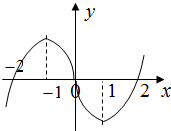
| A、(-∞,-1)∪(0,1) |
| B、(-1,0)∪(1,+∞) |
| C、(-2,-1)∪(1,2) |
| D、(-∞,-2)∪(2,+∞) |
考点:导数的运算,其他不等式的解法
专题:导数的概念及应用,不等式的解法及应用
分析:讨论x的符号,根据函数单调性和导数之间的关系即可得到结论.
解答:
解:若x=0时,不等式x•f′(x)<0不成立.
若x>0,则不等式x•f′(x)<0等价为f′(x)<0,此时函数单调递减,由图象可知,此时0<x<1.
若x<0,则不等式x•f′(x)<0等价为f′(x)>0,此时函数单调递增,由图象可知,此时x<-1.,
故不等式x•f′(x)<0的解集为(-∞,-1)∪(0,1).
故选:A.
若x>0,则不等式x•f′(x)<0等价为f′(x)<0,此时函数单调递减,由图象可知,此时0<x<1.
若x<0,则不等式x•f′(x)<0等价为f′(x)>0,此时函数单调递增,由图象可知,此时x<-1.,
故不等式x•f′(x)<0的解集为(-∞,-1)∪(0,1).
故选:A.
点评:本题主要考查不等式的解法,利用函数单调性和导数之间的关系即可得到结论.

练习册系列答案
相关题目
已知平面向量的集合A到A的映射f:
→f(
)=
-2(
•
)
(
为常向量)满足f(
)•f(
)=
•
对任意
,
∈A恒成立,则
的坐标不可能是( )
| x |
| x |
| x |
| x |
| a |
| a |
| a |
| x |
| y |
| x |
| y |
| x |
| y |
| a |
| A、(0,0) | ||||||||
B、(
| ||||||||
C、(-
| ||||||||
D、(
|
两直线ρsin(θ+
)=11,ρsin(θ-
)=10的位置关系是( )
| π |
| 4 |
| π |
| 4 |
| A、垂直 | B、平行 |
| C、斜交 | D、以上都不正确 |
参数方程为
(t为参数)的曲线C的普通方程为( )
|
| A、y=-2x+3 |
| B、y=-2x+3(x≥0) |
| C、y=-2x+3(x>1) |
| D、y=-2x+3(x≥1) |
已知回归方程
=1.5x-2,则原始数据(2,2)的残差
为( )
| ∧ |
| y |
| ∧ |
| e |
| A、-1 | B、1 | C、0 | D、0.5 |
下列命题错误的是( )
| A、若p或q为假命题,则p,q均为假命题 |
| B、命题“若x2-3x+2=0,则x=1”的逆否命题为“若x≠1,则x2-3x+2≠0” |
| C、若某一集合有4个元素,那么它真子集的个数共有24个 |
| D、?x∈Z,x3<1 |
用1,2,3,4,5排成一个五位数,则使任两个相邻数码之差至少是2的概率是( )
A、
| ||
B、
| ||
C、
| ||
D、
|