题目内容
已知sinα=-
,180°<α<270°,求sin
,cos
和tan
的值.
| 4 |
| 5 |
| α |
| 2 |
| α |
| 2 |
| α |
| 2 |
考点:二倍角的余弦,三角函数的化简求值,二倍角的正弦
专题:三角函数的求值
分析:根据角的范围,确定
的范围,求出余弦函数值,确定tan
的值的符号,转化为正弦函数与余弦函数值,然后化直线函数为正切函数,即可求解.
| α |
| 2 |
| α |
| 2 |
解答:
解:sinα=-
,180°<α<270°,cosα=-
=-
.
∵180°<α<270°,900<
<135°,∴tan
<0;
若tan
=
=
=
=
=
=-2,
(sin
)2=
=
=
,sin
=
,
cos
=-
=-
.
| 4 |
| 5 |
| 1-sin2α |
| 3 |
| 5 |
∵180°<α<270°,900<
| α |
| 2 |
| α |
| 2 |
若tan
| α |
| 2 |
sin
| ||
cos
|
sin
| ||||
cos2
|
| ||
cos2
|
| sinα |
| cosα+1 |
-
| ||
1-
|
(sin
| α |
| 2 |
sin2
| ||||
sin2
|
tan2
| ||
tan2
|
| 4 |
| 5 |
| α |
| 2 |
2
| ||
| 5 |
cos
| α |
| 2 |
1-sin2
|
| ||
| 5 |
点评:本题考查任意角的三角函数的定义,半角的三角函数,考查计算推理能力,是中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知α是第二象限角,则
是第几象限角( )
| α |
| 3 |
| A、第一或二象限 |
| B、第二或四象限 |
| C、第一或三或四象限 |
| D、第一或二或四象限 |
在等比数列{an}中,已知a3+a6=9,a2a7=8,则a32+a62=( )
| A、9 | B、65 | C、72 | D、99 |
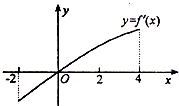 定义在[-2,+∞)的函数f(x)的部分值如下表,f(x)的导函数f(x)的图象如图,两正数a,b满足f(2a+b)<1,则
定义在[-2,+∞)的函数f(x)的部分值如下表,f(x)的导函数f(x)的图象如图,两正数a,b满足f(2a+b)<1,则| b+3 |
| a+3 |
A、(
| ||||
B、(
| ||||
C、(
| ||||
D、(-
|
在正方体ABCD-A1B1C1D1中与AD1成600角的面对角线的条数是( )
| A、4条 | B、6条 | C、8条 | D、10条 |
曲线C经过伸缩变换
后,对应曲线的方程为:x2+y2=1,则曲线C的方程为( )
|
A、
| ||||
B、4x2=
| ||||
C、
| ||||
| D、4x2+9y2=1 |