题目内容
曲线C经过伸缩变换
后,对应曲线的方程为:x2+y2=1,则曲线C的方程为( )
|
A、
| ||||
B、4x2=
| ||||
C、
| ||||
| D、4x2+9y2=1 |
考点:平面直角坐标轴中的伸缩变换
专题:坐标系和参数方程
分析:直角坐标系中的伸缩变换只要是利用变换前的关系式,变换关系,变换后的关系式,只要知道其中的两个变量就可以求出点三个变量.本题知道第二、第三个变量求第一个变量.
解答:
解:曲线C经过伸缩变换
①后,对应曲线的方程为:x′2+y′2=1②,
把①代入②得到:
+9y2=1
故选:A
|
把①代入②得到:
| x2 |
| 4 |
故选:A
点评:本题考查的知识要点:直角坐标系中的函数关系式的伸缩变换,属于基础题型.

练习册系列答案
相关题目
下列结论中,正确的是( )
①汽车的重量和汽车每消耗1升汽油所行驶的平均路程成正相关关系; ②散点图能直观地反映数据的相关程度; ③在统计中,众数不一定是数据组中数据; ④在统计中,样本的标准差越大说明这组数据的波动越大; ⑤概率是随机的,在试验前不能确定.
①汽车的重量和汽车每消耗1升汽油所行驶的平均路程成正相关关系; ②散点图能直观地反映数据的相关程度; ③在统计中,众数不一定是数据组中数据; ④在统计中,样本的标准差越大说明这组数据的波动越大; ⑤概率是随机的,在试验前不能确定.
| A、①③ | B、②⑤ | C、②④ | D、④⑤ |
已知函数f(x)=x2的图象如图所示,且点A、B、C、D在图象上,问函数f(x)=x2在哪点附近增长最快( )

| A、A点 | B、B点 | C、C点 | D、D点 |
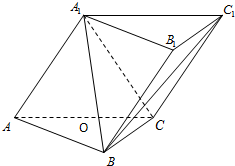 如图,三棱柱ABC-A1B1C1中,侧面AA1CC1垂直于底面ABC,AA1=A1C=AC=2,AB=BC,且AB⊥BC,O为AC中点.
如图,三棱柱ABC-A1B1C1中,侧面AA1CC1垂直于底面ABC,AA1=A1C=AC=2,AB=BC,且AB⊥BC,O为AC中点.