题目内容
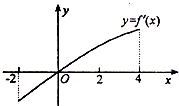定义在[-2，+∞）的函数f（x）的部分值如下表，f（x）的导函数f（x）的图象如图，两正数a，b满足f（2a+b）＜1，则| b+3 |
| a+3 |
A、(
| ||||
B、(
| ||||
C、(
| ||||
D、(-
|
考点：简单线性规划的应用
专题：不等式的解法及应用
分析：根据函数的单调性和导数之间的关系，得到关于a，b的不等式关系，利用线性规划的知识即可得到结论．
解答：
解：由f（x）的导函数f（x）的图象可得，当x∈[-2，0]，f（x）递减
当x∈[0．+∞]，f（x）递增．且f（2a+b）＜f（4）（a，b∈R+）
，
则
的几何意义是动点A（a，b）与定点（-3，-3）连线的斜率，
由线性规划可知
的取值范围为(
，
)，
故选：B
解：由f（x）的导函数f（x）的图象可得，当x∈[-2，0]，f（x）递减当x∈[0．+∞]，f（x）递增．且f（2a+b）＜f（4）（a，b∈R+）
|
则
| b+3 |
| a+3 |
由线性规划可知
| b+3 |
| a+3 |
| 3 |
| 5 |
| 7 |
| 3 |
故选：B
点评：本题主要考查线性规划的应用，利用圆函数单调性和导数之间的关系将条件进行转化是解决本题的关键．
练习册系列答案
相关题目
下列命题中，正确的是（ ）
A、x+
| ||||||
B、
| ||||||
| C、如果a＞b，c＞d，那么a-c＜b-d | ||||||
| D、如果ac2＞bc2，那么a＞b |
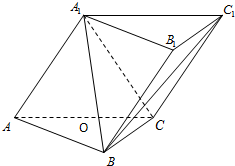如图，三棱柱ABC-A1B1C1中，侧面AA1CC1垂直于底面ABC，AA1=A1C=AC=2，AB=BC，且AB⊥BC，O为AC中点．