题目内容
某厂计划生产甲、乙两种产品，甲产品售价50千元/件，乙产品售价30千元/件，生产这两种产品需要A、B两种原料，生产甲产品需要A种原料4吨/件，B种原料2吨/件，生产乙产品需要A种原料3吨/件，B种原料1吨/件，该厂能获得A种原料120吨，B种原料50吨．问生产甲、乙两种产品各多少件时，能使销售总收入最大？最大总收入为多少？
考点：简单线性规划的应用
专题：不等式的解法及应用
分析：设生产甲、乙两种产品分别为x，y件时，能使销售总收入最大，根据条件建立不等式组，利用线性规划的知识即可得到结论．
解答：
解：设生产甲、乙两种产品分别为x，y件时，能使销售总收入最大，则z=50x+30y，
建立约束条件为
，
作出不等式组对应的平面区域如图：
平移直线50x+30y=0，即5x+3y=0，
则由图象可知当直线z=50x+30y经过点A时，
z取得最大值，
由
，解得
，
解A（10，20）
即z=50×10+30×20=1100，
即生产甲、乙两种产品分别为10件、20件，总收入最大是1100千元．
建立约束条件为
|
作出不等式组对应的平面区域如图：
平移直线50x+30y=0，即5x+3y=0，
则由图象可知当直线z=50x+30y经过点A时，
z取得最大值，
由
|
|
解A（10，20）
即z=50×10+30×20=1100，
即生产甲、乙两种产品分别为10件、20件，总收入最大是1100千元．
点评：本题主要考查线性规划的应用，根据条件建立不等式组，利用数形结合是解决本题的关键．
练习册系列答案
相关题目
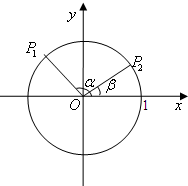如图在单位圆中，已知α、β是坐标平面内的任意两个角，且0≤α-β≤π，
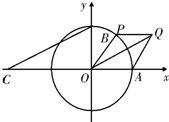如图所示，A，B分别是单位圆与x轴、y轴正半轴的交点，点P在单位圆上，∠AOP=θ（0＜θ＜π），C点坐标为（-2，0），平行四边形OAQP的面积为S．