题目内容
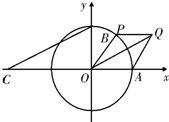 如图所示,A,B分别是单位圆与x轴、y轴正半轴的交点,点P在单位圆上,∠AOP=θ(0<θ<π),C点坐标为(-2,0),平行四边形OAQP的面积为S.
如图所示,A,B分别是单位圆与x轴、y轴正半轴的交点,点P在单位圆上,∠AOP=θ(0<θ<π),C点坐标为(-2,0),平行四边形OAQP的面积为S.(1)求
| OA |
| OQ |
(2)若CB∥OP,求sin(2θ-
| π |
| 6 |
考点:任意角的三角函数的定义,单位圆与周期性
专题:三角函数的求值
分析:(1)求出A(1,0),B(0,1).P(cos θ,sin θ),然后求解
•
,以及平行四边形OAQP的面积,通过两角和与差的三角函数,以及正弦函数的值域求解即可.
(2)利用三角函数的定义,求出sinθ,cosθ,利用二倍角公式以及两角和与差的三角函数求解表达式的值.
| OA |
| OQ |
(2)利用三角函数的定义,求出sinθ,cosθ,利用二倍角公式以及两角和与差的三角函数求解表达式的值.
解答:
解:(1)由已知,得A(1,0),B(0,1).P(cos θ,sin θ),因为四边形OAQP是平行四边形,
所以
=
+
=(1+cosθ,sinθ).
所以
•
=1+cosθ.(3分)
又平行四边形OAQP的面积为
S=|
•
|sin θ=sin θ,
所以
•
+S=1+cosθ+sin θ=
sin(θ+
)+1.(5分)
又0<θ<π,
所以当θ=
时,
•
+S的最大值为
+1.(7分)
(2)由题意,知
=(2,1),
=(cosθ,sinθ),
因为CB∥OP,所以cosθ=2sinθ.
又0<θ<π,cos2θ+sin2θ=1,
解得sin θ=
,cos θ=
,
所以sin2θ=2sin θcosθ=
,cos 2θ=cos2θ-sin2θ=
.
所以sin(2θ-
)=sin 2θcos
-cos 2θsin
=
×
-
×
=
.(13分)
所以
| OQ |
| OA |
| OP |
所以
| OA |
| OQ |
又平行四边形OAQP的面积为
S=|
| OA |
| OP |
所以
| OA |
| OQ |
| 2 |
| π |
| 4 |
又0<θ<π,
所以当θ=
| π |
| 4 |
| OA |
| OQ |
| 2 |
(2)由题意,知
| CB |
| OP |
因为CB∥OP,所以cosθ=2sinθ.
又0<θ<π,cos2θ+sin2θ=1,
解得sin θ=
| ||
| 5 |
2
| ||
| 5 |
所以sin2θ=2sin θcosθ=
| 4 |
| 5 |
| 3 |
| 5 |
所以sin(2θ-
| π |
| 6 |
| π |
| 6 |
| π |
| 6 |
| 4 |
| 5 |
| ||
| 2 |
| 3 |
| 5 |
| 1 |
| 2 |
4
| ||
| 10 |
点评:本题考查三角函数的定义,两角和与差的三角函数,三角函数的求值与化简.

练习册系列答案
相关题目