Question

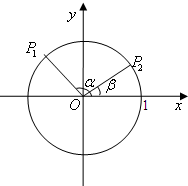如图在单位圆中，已知α、β是坐标平面内的任意两个角，且0≤α-β≤π，
请写出两角差的余弦公式并加以证明．

Answer 1

考点：两角和与差的余弦函数

专题：证明题

分析：设P₁（cosα，sinα），P₂（cosβ，sinβ），则

OP1

=（cosα，sinα），

OP2

=（cosβ，sinβ），利用向量的数量积的坐标运算及定义即可证得结论

解答： 解：两角差的余弦公式为：cos（α-β）=cosαcosβ+sinαsinβ  …（6分）
证明：设P₁（cosα，sinα），P₂（cosβ，sinβ），
则

OP1

=（cosα，sinα），

OP2

=（cosβ，sinβ），
因为

OP1

•

OP2

=cosαcosβ+sinαsinβ，
又因为

OP1

•

OP2

=|

OP1

|•|

OP2

|cos（α-β）=1×1cos（α-β）=cos（α-β）．
所以cos（α-β）=cosαcosβ+sinαsinβ．…（14分）

点评：本题考查两角和与差的余弦函数，考查向量的数量积的坐标运算及数量积的概念，属于中档题．