题目内容
已知实数a＞0且a≠1，函数f（x）=
，若数列{an}满足an=f（n）（n∈N*），且{an}是等差数列，则a= ，b= ．
|
考点：分段函数的应用
专题：函数的性质及应用
分析：分别表示出数列{an}的前四项，由{an}是等差数列，求出a，b的值．
解答：
解：n=1时，a1=a，
n=2时，a2=a2，
n=3时，a3=3a+b，
n=4时，a4=4a+b，
∵{an}是等差数列，
∴d=a=a2-a，
解得：a=0（舍），a=2，
∴a1=2，a2=4，a3=6=3a+b，
∴b=0．
故答案为：2，0．
n=2时，a2=a2，
n=3时，a3=3a+b，
n=4时，a4=4a+b，
∵{an}是等差数列，
∴d=a=a2-a，
解得：a=0（舍），a=2，
∴a1=2，a2=4，a3=6=3a+b，
∴b=0．
故答案为：2，0．
点评：本题考察了分段函数问题，等差数列的性质，是一道基础题．
练习册系列答案
口算题卡加应用题集训系列答案
综合自测系列答案
相关题目
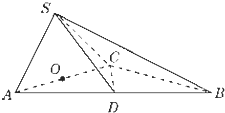已知三棱锥S-ABC中，平面ASC⊥平面ABC，O、D分别为AC、AB的中点，AS=CS=CD=AD=