题目内容
已知函数f(x)=x2-3x+alnx(a>0).
(I)若a=1,求函数f(x)的单调区间和极值;
(Ⅱ)若曲线y=f(x)的切线斜率的最小值为1,求a的值.
(I)若a=1,求函数f(x)的单调区间和极值;
(Ⅱ)若曲线y=f(x)的切线斜率的最小值为1,求a的值.
考点:利用导数研究函数的极值,利用导数研究函数的单调性,利用导数研究曲线上某点切线方程
专题:
分析:(Ⅰ)把a=1代入原函数解析式,求导后由导函数大于0求得原函数的增区间,由导函数小于0求得原函数的减区间,从而得到极值点并求得极值;
(Ⅱ)由f(x)=2x-3+
的最小值为1,由a>0得,2x-3+
≥2
-3=2
-3,从而求出a的值.
(Ⅱ)由f(x)=2x-3+
| a |
| x |
| a |
| x |
2x•
|
| 2a |
解答:
解:(I)f(x)的定义域为(0,+∞),
当a=1时,f(x)=x2-3x+lnx,
f(x)=
=
,
由2x2-3x+1=0,得x1=1x2=
,
由2x2-3x+1>0,得x<
,或x>1,∴f(x)的单调递增区间为(0,
),(1,+∞).
由2x2-3x+1<0,得
<x<1,∴f(x)的单调递减区间为(
,1).
∴f(x)极大值为f(
)=-
-ln2;极小值为f(1)=-2;
(Ⅱ)由f(x)=2x-3+
的最小值为1,
由a>0得,2x-3+
≥2
-3=2
-3,
∴2
-3=1,
∴a=2.
当a=1时,f(x)=x2-3x+lnx,
f(x)=
| 2x2-3x+1 |
| x |
| (2x-1)(x-1) |
| x |
由2x2-3x+1=0,得x1=1x2=
| 1 |
| 2 |
由2x2-3x+1>0,得x<
| 1 |
| 2 |
| 1 |
| 2 |
由2x2-3x+1<0,得
| 1 |
| 2 |
| 1 |
| 2 |
∴f(x)极大值为f(
| 1 |
| 2 |
| 5 |
| 4 |
(Ⅱ)由f(x)=2x-3+
| a |
| x |
由a>0得,2x-3+
| a |
| x |
2x•
|
| 2a |
∴2
| 2a |
∴a=2.
点评:本题考察了函数的单调性,导数的应用,极值的求法,是一道中档题.

练习册系列答案
相关题目
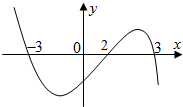 若连续函数f(x)在R上可导,其导函数为f′(x),且函数y=(2-x)f′(x)的图象如图所示,则下列结论中一定成立的是( )
若连续函数f(x)在R上可导,其导函数为f′(x),且函数y=(2-x)f′(x)的图象如图所示,则下列结论中一定成立的是( )| A、f(x)有极大值f(3)和极小值f(2) |
| B、f(x)有极大值f(-3)和极小值f(2) |
| C、f(x)有极大值f(3)和极小值f(-3) |
| D、f(x)有极大值f(-3)和极小值f(3) |
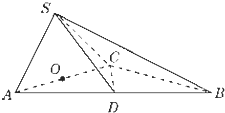 已知三棱锥S-ABC中,平面ASC⊥平面ABC,O、D分别为AC、AB的中点,AS=CS=CD=AD=
已知三棱锥S-ABC中,平面ASC⊥平面ABC,O、D分别为AC、AB的中点,AS=CS=CD=AD=