题目内容
已知数列{an}的前n项和为Sn=3n,数列{bn}满足b1=-1,bn+1=bn+2n-1(n∈N*).
(1)求数列{an}的通项公式;
(2)求数列{bn}的通项公式;
(3)求
+
+
+…+
的值.
(1)求数列{an}的通项公式;
(2)求数列{bn}的通项公式;
(3)求
| 1 |
| b3 |
| 1 |
| b4 |
| 1 |
| b5 |
| 1 |
| bn |
考点:数列的求和,数列递推式
专题:等差数列与等比数列
分析:(1)利用公式an=
,由已知条件能求出数列{an}的通项公式.
(2)由bn+1=bn+2n-1,利用累加法能求出bn=n2-2n.
(3)由
=
=
(
-
),利用裂项求和法能求出
+
+
+…+
的值.
|
(2)由bn+1=bn+2n-1,利用累加法能求出bn=n2-2n.
(3)由
| 1 |
| bn |
| 1 |
| n2-2n |
| 1 |
| 2 |
| 1 |
| n-2 |
| 1 |
| n |
| 1 |
| b3 |
| 1 |
| b4 |
| 1 |
| b5 |
| 1 |
| bn |
解答:
解:(1)∵Sn=3n,∴Sn-1=3n-1,(n≥2),
∴an=Sn-Sn-1=3n-3n-1=2•3n-1,(n≥2)
当n=1时,a1=s1=3≠2×30,
∴an=
.
(2)∵bn+1=bn+2n-1
∴b2-b1=1,b3-b2=3,b4-b3=5,…,bn-bn-1=2n-3
以上各式相加得:
bn-b1=1+3+5+…+(2n-3)
=
=(n-1)2,
∵b1=-1,∴bn=n2-2n.
(3)∵
=
=
(
-
)(n≥3)
∴
+
+
+…+
=
(
-
+
-
+
-
+…+
-
)
=
(1+
-
-
)=
.
∴an=Sn-Sn-1=3n-3n-1=2•3n-1,(n≥2)
当n=1时,a1=s1=3≠2×30,
∴an=
|
(2)∵bn+1=bn+2n-1
∴b2-b1=1,b3-b2=3,b4-b3=5,…,bn-bn-1=2n-3
以上各式相加得:
bn-b1=1+3+5+…+(2n-3)
=
| (n-1)(1+2n-3) |
| 2 |
∵b1=-1,∴bn=n2-2n.
(3)∵
| 1 |
| bn |
| 1 |
| n2-2n |
| 1 |
| 2 |
| 1 |
| n-2 |
| 1 |
| n |
∴
| 1 |
| b3 |
| 1 |
| b4 |
| 1 |
| b5 |
| 1 |
| bn |
| 1 |
| 2 |
| 1 |
| 3-2 |
| 1 |
| 3 |
| 1 |
| 4-2 |
| 1 |
| 4 |
| 1 |
| 5-2 |
| 1 |
| 5 |
| 1 |
| n-2 |
| 1 |
| n |
=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| n-1 |
| 1 |
| n |
| 3n2-7n+2 |
| 4n2-4n |
点评:本题考查数列的通项公式的求法,考查数列的前n项和的求法,解题时要注意累加法和裂项求和法的合理运用.

练习册系列答案
 寒假学与练系列答案
寒假学与练系列答案
相关题目
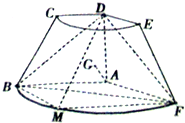 如图,在直角梯形ABCD中,AB=AD=2,把此梯形绕其直角边AD旋转120°得到如图所示的几何体,点G是∠BDF平分线上任意一点(异于点D),点M是弧
如图,在直角梯形ABCD中,AB=AD=2,把此梯形绕其直角边AD旋转120°得到如图所示的几何体,点G是∠BDF平分线上任意一点(异于点D),点M是弧
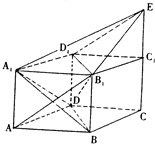 如图,已知直四棱柱ABCD-A1B1C1D1中,AB=AA1,底面ABCD为菱形,∠ADC=120°,E为CC1延长线上一点.
如图,已知直四棱柱ABCD-A1B1C1D1中,AB=AA1,底面ABCD为菱形,∠ADC=120°,E为CC1延长线上一点.