题目内容
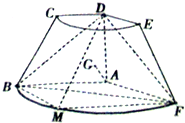 如图,在直角梯形ABCD中,AB=AD=2,把此梯形绕其直角边AD旋转120°得到如图所示的几何体,点G是∠BDF平分线上任意一点(异于点D),点M是弧
如图,在直角梯形ABCD中,AB=AD=2,把此梯形绕其直角边AD旋转120°得到如图所示的几何体,点G是∠BDF平分线上任意一点(异于点D),点M是弧 |
| BF |
(Ⅰ)求证:BF⊥AG;
(Ⅱ)求三棱锥M-BDF的体积VM-BDF.
考点:棱柱、棱锥、棱台的体积
专题:综合题,空间位置关系与距离
分析:(Ⅰ)连接AM交BF于点O,证明AM⊥BF,DA⊥BF,可得BF⊥平面ADM,从而BF⊥AG;
(Ⅱ)利用VM-BDF=VD-BMF,求三棱锥M-BDF的体积VM-BDF.
(Ⅱ)利用VM-BDF=VD-BMF,求三棱锥M-BDF的体积VM-BDF.
解答:
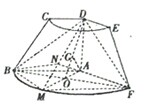 (Ⅰ)证明:连接AM交BF于点O,则
(Ⅰ)证明:连接AM交BF于点O,则
∵点M是弧
的中点,
∴AM⊥BF且O为BF的中点,
∵DB=DF,
∴DO平分∠BDF,即点G在直线DO上,
∵DA⊥AB,DA⊥AF,AB∩AF=A,
∴DA⊥平面ABF,
∴DA⊥BF,
∵DA∩AM=A,
∴BF⊥平面ADM,
∵AG?平面ADM,
∴BF⊥AG;
(Ⅱ)解:由已知,AB=2,∠BAM=60°,∠AOB=90°,
∴AO=OM=1,BF=2
,
∴S△BMF=
BF•OM=
,
∴VM-BDF=VD-BMF=
•
•2=
 (Ⅰ)证明:连接AM交BF于点O,则
(Ⅰ)证明:连接AM交BF于点O,则∵点M是弧
 |
| BF |
∴AM⊥BF且O为BF的中点,
∵DB=DF,
∴DO平分∠BDF,即点G在直线DO上,
∵DA⊥AB,DA⊥AF,AB∩AF=A,
∴DA⊥平面ABF,
∴DA⊥BF,
∵DA∩AM=A,
∴BF⊥平面ADM,
∵AG?平面ADM,
∴BF⊥AG;
(Ⅱ)解:由已知,AB=2,∠BAM=60°,∠AOB=90°,
∴AO=OM=1,BF=2
| 3 |
∴S△BMF=
| 1 |
| 2 |
| 3 |
∴VM-BDF=VD-BMF=
| 1 |
| 3 |
| 3 |
2
| ||
| 3 |
点评:本题考查与二面角有关的立体几何综合问题,考查直线与平面垂直的判定与性质,考查三棱锥M-BDF的体积,属于中档题.

练习册系列答案
相关题目
设x>0,y>0,x+y-x2y2=4,则
+
的最小值等于( )
| 1 |
| x |
| 1 |
| y |
| A、2 | ||
| B、4 | ||
C、
| ||
D、
|
边长为2的正方形的直观图的周长为( )
| A、8 | B、12 | C、10 | D、6 |
 某成品的组装工序流程图如图所示,箭头上的数字表示组装过程中所需要的时间(小时),不同车间可同时工作,同一车间不能同时做两种或两种以上的工作,则组装该产品所需要的最短时间是( )
某成品的组装工序流程图如图所示,箭头上的数字表示组装过程中所需要的时间(小时),不同车间可同时工作,同一车间不能同时做两种或两种以上的工作,则组装该产品所需要的最短时间是( )| A、11小时 | B、13小时 |
| C、15小时 | D、10小时 |
一个口袋内有大小、形状相同的6个白球和5个黑球,从中随机取出3个球,则至少取到2个白球的概率为( )
A、
| ||
B、
| ||
C、
| ||
D、
|