题目内容

已知3a2+2b2=5，试求y=
2a2+1
•
b2+2
的最大值．
考点：基本不等式
专题：不等式的解法及应用
分析：先提取出
4
3
，进而利用基本不等式求得y的最大值．
解答： 解：y=
4
3
•
3
2
a2+
3
4
•
b2+2
≤
2
3
3
•
3
2
a2+
3
4
+b2+2
2
=
2
3
3
×
21
4
2
=
7
3
4
，
3
2
a2+
3
4
=b2+2时取等号．
点评：本题主要考查了基本不等式的运用．解题的关键是利用已知构造出和为定值来．
练习册系列答案
相关题目
已知平面直角坐标系中，点O为原点，A（-3，-4），B（5，-12），若
OC
=
OA
+
OB
，
OD
=
OA
-
OB
．
（Ⅰ）求点C和点D的坐标；
（Ⅱ）求
OC
•
OD
．
如图，已知PA⊥⊙O所在的平面，AB是⊙O的直径，AB=2，C是⊙O上一点，且AC=BC，PC与⊙O所在的平面成45°角，E是PC中点．
（Ⅰ）求证：AE⊥PB；
（Ⅱ）求PB与面PAC所成角的正切值；
（Ⅲ）求异面直线PB与AC所成角的余弦值．
已知数列{an}的前n项和为Sn=3n，数列{bn}满足b1=-1，bn+1=bn+2n-1（n∈N*）．
（1）求数列{an}的通项公式；
（2）求数列{bn}的通项公式；
（3）求
1
b3
+
1
b4
+
1
b5
+…+
1
bn
的值．
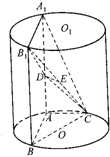如图，AA1、BB1为圆柱OO1的母线，BC是底面圆O的直径，D、E分别是AA1、CB1的中点，AB=AC．
（Ⅰ）证明：DE∥平面ABC；
（Ⅱ）证明：平面B1DC⊥平面CBB1．
设函数f（x）=（ax2-2x）•ex，其中a≥0．
（Ⅰ）当a=
4
3
时，求f（x）的极值点；
（Ⅱ）若f（x）在[-1，1]上为单调函数，求a的取值范围．
为了了解青少年视力情况，某市从高考体检中随机抽取16名学生的视力进行调查，经医生用对数视力表检查得到每个学生的视力状况的茎叶图（以小数点前的一位数字为茎，小数点后的一位数字为叶）如图所示．
（1）若视力测试结果不低丁5.0，则称为“好视力”，求校医从这16人中随机选取3人，至多有1人是“好视力”的概率；
（2）以这16人的样本数据来估计该市所有参加高考学生的总体数据，若从该市参加高考的学生中任选3人，记ξ表示抽到“好视力”学生的人数，求ξ的分布列及数学期望．
△ABC中，
5
sin2A-（2
5
+1）sinA+2=0，A是锐角，求cot2A的值．
有下列命题：
①在函数y=cos（x-
π
4
）cos（x+
π
4
）的图象中，相邻两个对称中心的距离为
π
2
；
②若锐角α，β满足cosα＞sinβ，则α+β＜
π
2
；
③若α，β均为第一象限角，且α＞β，则sinα＞sinβ；
④要得到函数y=sin（
x
2
-
π
4
）的图象，只需将y=sin
x
2
的图象向右平移
π
4
个单位；
则以上所有真命题的序号是
 
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网