题目内容
已知函数f(x)=
x2-(m+1)x+mlnx,m>0.
(Ⅰ)求f(x)的单调区间;
(Ⅱ)设点A(x0,f(x0))(x0>1)为f(x)的图象上任意一点,若曲线y=f(x)在点A处的切线的斜率恒大于-1,求m的取值范围.
| 1 |
| 2 |
(Ⅰ)求f(x)的单调区间;
(Ⅱ)设点A(x0,f(x0))(x0>1)为f(x)的图象上任意一点,若曲线y=f(x)在点A处的切线的斜率恒大于-1,求m的取值范围.
考点:利用导数研究曲线上某点切线方程,利用导数研究函数的单调性
专题:导数的综合应用
分析:(Ⅰ)求函数的导数,利用函数单调性和导数之间的关系,即可求f(x)的单调区间;
(Ⅱ)求函数的导数,根据导数的几何意义,解不等式即可得到结论.
(Ⅱ)求函数的导数,根据导数的几何意义,解不等式即可得到结论.
解答:
解:(Ⅰ) 依题意,f(x)的定义域为(0,+∞),f′(x)=x-(m+1)+
=
=
,
令f'(x)=0得x=m或x=1.
①当0<m<1时,f(x)在(0,m)递增,(m,1)递减,(1,+∞)递增;
②当m=1时,f'(x)≥0恒成立,所以f(x)在(0,+∞)递增;
③当m>1时,f(x)在(0,1)递增,(1,m)递减,(m,+∞)递增;
(Ⅱ)因为函数f(x)在点A(x0,f(x0))处的切线的斜率大于-1,
所以当x0∈(1,+∞)时,f′(x)=x0-(m+1)+
>-1恒成立,
即当x0∈(1,+∞)时,x02-mx0+m>0恒成立.
因x02-mx0+m>0⇒x02>m(x0-1),
当x0>1时x02>m(x0-1)等价于m<
.
设g(x0)=
=
=(x0-1)+
+2≥4(x0=2时取等号)
则在(1,+∞)上,当0<m<4时,
在函数f(x)的图象上任意一点A处的切线的斜率恒大于-1.
注:构造二次函数,比较
与1的大小也可得0<m<4.
| m |
| x |
| x2-(m+1)x+m |
| x |
| (x-m)(x-1) |
| x |
令f'(x)=0得x=m或x=1.
①当0<m<1时,f(x)在(0,m)递增,(m,1)递减,(1,+∞)递增;
②当m=1时,f'(x)≥0恒成立,所以f(x)在(0,+∞)递增;
③当m>1时,f(x)在(0,1)递增,(1,m)递减,(m,+∞)递增;
(Ⅱ)因为函数f(x)在点A(x0,f(x0))处的切线的斜率大于-1,
所以当x0∈(1,+∞)时,f′(x)=x0-(m+1)+
| m |
| x0 |
即当x0∈(1,+∞)时,x02-mx0+m>0恒成立.
因x02-mx0+m>0⇒x02>m(x0-1),
当x0>1时x02>m(x0-1)等价于m<
| x02 |
| x0-1 |
设g(x0)=
| x02 |
| x0-1 |
| (x0-1)2+2(x0-1)+1 |
| x0-1 |
| 1 |
| x0-1 |
则在(1,+∞)上,当0<m<4时,
在函数f(x)的图象上任意一点A处的切线的斜率恒大于-1.
注:构造二次函数,比较
| m |
| 2 |
点评:本题主要考查函数的单调区间的求解,以及导数的几何意义,考查导数的基本运算.

练习册系列答案
相关题目
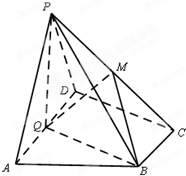 如图,在四棱锥P-ABCD中,底面ABCD为直角梯形,AD∥BC,∠ADC=90°,平面PAD⊥底面ABCD,Q为AD的中点,M是棱PC上的点,PA=PD=2,BC=
如图,在四棱锥P-ABCD中,底面ABCD为直角梯形,AD∥BC,∠ADC=90°,平面PAD⊥底面ABCD,Q为AD的中点,M是棱PC上的点,PA=PD=2,BC=