题目内容
一个盒子中装有6个小球,其中红色球4个,编号分别为1,2,3,4;白色球2个,编号分别为3,4,现从盒子中任取3个小球(假设每个小球从盒中被取出的可能性相同)
(Ⅰ)求取出的3个球中的编号最大数值为3的概率;
(Ⅱ)在取出的3个球中,记红色球编号最大数值为ξ,求ξ的分布列与数学期望.
(Ⅰ)求取出的3个球中的编号最大数值为3的概率;
(Ⅱ)在取出的3个球中,记红色球编号最大数值为ξ,求ξ的分布列与数学期望.
考点:离散型随机变量的期望与方差,古典概型及其概率计算公式
专题:概率与统计
分析:(Ⅰ)设“取出的3个球中编号最大数值为3的球”为事件A,则最大数值为3相当于从编号为1,2,3的红色球和编号为3的白色球中任取3个,由此能求出其概率.
(Ⅱ)ξ的可能取值为1,2,3,4,分别求出相应的概率,由此能求出ξ的分布列与数学期望.
(Ⅱ)ξ的可能取值为1,2,3,4,分别求出相应的概率,由此能求出ξ的分布列与数学期望.
解答:
解:(Ⅰ)设“取出的3个球中编号最大数值为3的球”为事件A,
则最大数值为3相当于从编号为1,2,3的红色球和编号为3的白色球中任取3个,
其概率P(A)=
=
. …(4分)
(Ⅱ)ξ的可能取值为1,2,3,4,…(5分)
P(ξ=1)=
=
,
P(ξ=2)=
=
,
P(ξ=3)=
=
,
P(ξ=4)=
=
,
所以ξ的分布列为 …(9分)
故Eξ=1×
+2×
+3×
+4×
=
.…(12分)
则最大数值为3相当于从编号为1,2,3的红色球和编号为3的白色球中任取3个,
其概率P(A)=
| ||
|
| 1 |
| 5 |
(Ⅱ)ξ的可能取值为1,2,3,4,…(5分)
P(ξ=1)=
| 1 | ||
|
| 1 |
| 20 |
P(ξ=2)=
| ||
|
| 3 |
| 20 |
P(ξ=3)=
| ||
|
| 6 |
| 20 |
P(ξ=4)=
| ||
|
| 10 |
| 20 |
所以ξ的分布列为 …(9分)
| ξ | 1 | 2 | 3 | 4 | ||||||||
| P |
|
|
|
|
| 1 |
| 20 |
| 3 |
| 20 |
| 6 |
| 20 |
| 10 |
| 20 |
| 13 |
| 4 |
点评:本题考查概率的求法,考查离散型随机变量的分布列和数学期望的求法,是中档题.

练习册系列答案
相关题目
 某成品的组装工序流程图如图所示,箭头上的数字表示组装过程中所需要的时间(小时),不同车间可同时工作,同一车间不能同时做两种或两种以上的工作,则组装该产品所需要的最短时间是( )
某成品的组装工序流程图如图所示,箭头上的数字表示组装过程中所需要的时间(小时),不同车间可同时工作,同一车间不能同时做两种或两种以上的工作,则组装该产品所需要的最短时间是( )| A、11小时 | B、13小时 |
| C、15小时 | D、10小时 |
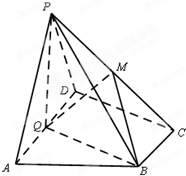 如图,在四棱锥P-ABCD中,底面ABCD为直角梯形,AD∥BC,∠ADC=90°,平面PAD⊥底面ABCD,Q为AD的中点,M是棱PC上的点,PA=PD=2,BC=
如图,在四棱锥P-ABCD中,底面ABCD为直角梯形,AD∥BC,∠ADC=90°,平面PAD⊥底面ABCD,Q为AD的中点,M是棱PC上的点,PA=PD=2,BC= 如图,已知PA⊥⊙O所在的平面,AB是⊙O的直径,AB=2,C是⊙O上一点,且AC=BC,PC与⊙O所在的平面成45°角,E是PC中点.
如图,已知PA⊥⊙O所在的平面,AB是⊙O的直径,AB=2,C是⊙O上一点,且AC=BC,PC与⊙O所在的平面成45°角,E是PC中点.