题目内容
设函数f(x)=(x-1)ex-kx2(x>0,k∈R).
(Ⅰ)谈论f(x)的单调性;
(Ⅱ)若当k>
时,f(x)+(ln2k)2+2kln
>0对?x∈(0,+∞)恒成立,求证:f(k-1+ln2)<f(k).
(Ⅰ)谈论f(x)的单调性;
(Ⅱ)若当k>
| 1 |
| 2 |
| e |
| 2k |
考点:利用导数研究函数的单调性,利用导数求闭区间上函数的最值
专题:导数的综合应用
分析:(Ⅰ)求函数的导数,利用函数的导数和单调性之间的关系,即可判断f(x)的单调性;
(Ⅱ)根据不等式恒成立,转化为求函数最值,即可证明不等式.
(Ⅱ)根据不等式恒成立,转化为求函数最值,即可证明不等式.
解答:
解:(Ⅰ)依题,f′(x)=xex-2kx=x(ex-2k),…(1分)
∵x>0,∴ex>1,
∴当2k≤1即k≤
时,f′(x)≥0恒成立,于是f(x)单调递增;
当2k>1即k>
时,由f′(x)=0,得x1=0(舍)x2=ln2k>0,
x∈(0,ln2k)时,f′(x)<0,f(x)单调递减;
x∈(ln2k,+∞)时,f′(x)>0,f(x)单调递增;…(4分)
综上,当k≤
时,f(x)的单增区间为(0,+∞),无单减区间;
当k>
时,f(x)的单增区间为(ln2k,+∞),单减区间(0,ln2k).
(Ⅱ)由(Ⅰ)知,k>
时,
f(x)min=f(ln2k)=(ln2k-1)eln2k-k(ln2k)2=2k(ln2k-1)-k(ln2k)2
又∵f(x)+(ln2k)2+2kln
>0,
对?x∈(0,+∞)恒成立,
即2k(ln2k-1)+(ln2k)2+2k(1-ln2k)-k(ln2k)2>0恒成立.…(7分)
∴(1-k)(ln2k)2>0.
又∵k>
,∴ln2k>0,∴k∈(
,1].
设g(k)=k+ln2-1-ln2k(
<k≤1),则g(k)=1-
=
<0
∴g(k)在(
,1]上单调递减,…(10分)
∴g(k)>g(1)=0,
即k+ln2-1-ln2k>0,而ln2-1<0,
∴k>k+ln2-1>ln2k,
由(Ⅰ)知,f(x)在(ln2k,+∞)上单调递增,
∴f(k-1+ln2)<f(k).
∵x>0,∴ex>1,
∴当2k≤1即k≤
| 1 |
| 2 |
当2k>1即k>
| 1 |
| 2 |
x∈(0,ln2k)时,f′(x)<0,f(x)单调递减;
x∈(ln2k,+∞)时,f′(x)>0,f(x)单调递增;…(4分)
综上,当k≤
| 1 |
| 2 |
当k>
| 1 |
| 2 |
(Ⅱ)由(Ⅰ)知,k>
| 1 |
| 2 |
f(x)min=f(ln2k)=(ln2k-1)eln2k-k(ln2k)2=2k(ln2k-1)-k(ln2k)2
又∵f(x)+(ln2k)2+2kln
| e |
| 2k |
对?x∈(0,+∞)恒成立,
即2k(ln2k-1)+(ln2k)2+2k(1-ln2k)-k(ln2k)2>0恒成立.…(7分)
∴(1-k)(ln2k)2>0.
又∵k>
| 1 |
| 2 |
| 1 |
| 2 |
设g(k)=k+ln2-1-ln2k(
| 1 |
| 2 |
| 1 |
| k |
| k-1 |
| k |
∴g(k)在(
| 1 |
| 2 |
∴g(k)>g(1)=0,
即k+ln2-1-ln2k>0,而ln2-1<0,
∴k>k+ln2-1>ln2k,
由(Ⅰ)知,f(x)在(ln2k,+∞)上单调递增,
∴f(k-1+ln2)<f(k).
点评:本题主要考查函数单调性的判断,以及利用导数证明不等式,综合性较强,运算量较大,有一定的难度.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
一个口袋内有大小、形状相同的6个白球和5个黑球,从中随机取出3个球,则至少取到2个白球的概率为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
 如图,已知PA⊥⊙O所在的平面,AB是⊙O的直径,AB=2,C是⊙O上一点,且AC=BC,PC与⊙O所在的平面成45°角,E是PC中点.
如图,已知PA⊥⊙O所在的平面,AB是⊙O的直径,AB=2,C是⊙O上一点,且AC=BC,PC与⊙O所在的平面成45°角,E是PC中点.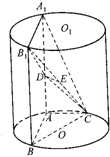 如图,AA1、BB1为圆柱OO1的母线,BC是底面圆O的直径,D、E分别是AA1、CB1的中点,AB=AC.
如图,AA1、BB1为圆柱OO1的母线,BC是底面圆O的直径,D、E分别是AA1、CB1的中点,AB=AC. 为了了解青少年视力情况,某市从高考体检中随机抽取16名学生的视力进行调查,经医生用对数视力表检查得到每个学生的视力状况的茎叶图(以小数点前的一位数字为茎,小数点后的一位数字为叶)如图所示.
为了了解青少年视力情况,某市从高考体检中随机抽取16名学生的视力进行调查,经医生用对数视力表检查得到每个学生的视力状况的茎叶图(以小数点前的一位数字为茎,小数点后的一位数字为叶)如图所示.