题目内容

证明：钝角三角形的内角中有且只有一个钝角．
考点：反证法与放缩法
专题：证明题,反证法
分析：假设钝角三角形的内角中至少有两个钝角，则三角形的内角和大于180°，与三角形的内角和等于180°矛盾，即可得出结论．
解答： 证明：假设钝角三角形的内角中至少有两个钝角，则三角形的内角和大于180°，
与三角形的内角和等于180°矛盾，
∴钝角三角形的内角中有且只有一个钝角．
点评：本题考查用反证法证明数学命题，把要证的结论进行否定，得到要证的结论的反面，是解题的突破口．
练习册系列答案
相关题目
设集合A={x||x-1|≤2}，B={x|log2x＜2}，则A∪B=（　　）
A、[-1，3]
B、[-1，4）
C、（0，3]
D、（-∞，4）
已知函数f（x）=x2-4x+a+3．
（1）当a=0时，求函数f（x）在区间[1，4]上的值域；
（2）若函数y=f（x）在区间[-1，1]上存在零点，求实数a的取值范围；
（3）设函数y=f（x）（x∈[t，4]）的值域为区间D，是否存在常熟t，使区间D的长度为9，？若存在，求出所有满足这个条件的t的值；若不存在，请说明理由．（注：区间[p，q]）
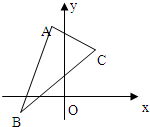如图，已知△ABC三个顶点是A（-1，4），B（-2，-1），C（2，3）
（1）若BC边的中间为D，求BC边中线AD所在的直线方程．
（2）过A作AE⊥BC于点E，求垂线AE所在的直线方程，求垂线AE的长度．
（3）记过点A的直线为l，若点C到直线l的距离为3，求直线的方程．
如图，已知圆柱体底面圆的半径为
2
π
 cm，高为2cm，AB，CD分别是两底面的直径，AD，BC是母线．若一只小虫从A点出发，从侧面爬行到C点，则小虫爬行的最短路线的长度是（　　）cm．（结果保留根式）（　　）
A、
2
3
3
B、2
3
C、2
2
D、4
已知函数f（x）=2sin（2x+
π
3
），x∈R．
（1）在给定的直角坐标系中，运用“五点法”画出该函数在x∈[-
π
6
，
5π
6
]的图象；
（2）若θ为锐角，且满足f（θ）-f（-θ）=1，求θ的值．
若y=f（x）是奇函数，当x＞0时，f（x）=2x+1，f（log2
1
3
）=
 
．
已知P1（x1，y1）是直线l：f（x，y）=0上的一点，P2（x2，y2）是直线l外一点，则方程f（x，y）+f（x1，y1）+f（x2，y2）=0表示的直线与直线l的位置关系是
 
．
已知数列{an}满足a1=1，a2n=a2n-1+（-1）n，a2n+1=a2n+3n（n∈N*），则数列{an}的前10项的和为
 
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网