题目内容
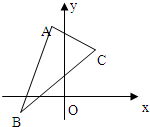 如图,已知△ABC三个顶点是A(-1,4),B(-2,-1),C(2,3)
如图,已知△ABC三个顶点是A(-1,4),B(-2,-1),C(2,3)(1)若BC边的中间为D,求BC边中线AD所在的直线方程.
(2)过A作AE⊥BC于点E,求垂线AE所在的直线方程,求垂线AE的长度.
(3)记过点A的直线为l,若点C到直线l的距离为3,求直线的方程.
考点:直线的一般式方程与直线的垂直关系,两点间的距离公式
专题:直线与圆
分析:(1)由中点坐标公式得D的坐标,然后利用两点式的BC边中线AD所在的直线方程;
(2)由两点求斜率可得kBC=
=1,进一步得到BC边上的高线AE的斜率为-1,再由直线方程的点斜式求得
AE所在直线方程;由B(-2,-1),C(2,3)可得BC边所在直线方程,由点到直线的距离公式求得A到BC的距离;
(3)当直线斜率不存在时,直线方程为x=-1,满足C到l的距离为3;当直线斜率存在时,设出直线方程,化为一般式后由点到直线的距离公式得k,代回直线方程得答案.
(2)由两点求斜率可得kBC=
| 3+1 |
| 2+2 |
AE所在直线方程;由B(-2,-1),C(2,3)可得BC边所在直线方程,由点到直线的距离公式求得A到BC的距离;
(3)当直线斜率不存在时,直线方程为x=-1,满足C到l的距离为3;当直线斜率存在时,设出直线方程,化为一般式后由点到直线的距离公式得k,代回直线方程得答案.
解答:
解:(1)∵B(-2,-1),C(2,3),
由中点坐标公式得D(0,1),
又A(-1,4),
∴BC边中线AD所在的直线方程为
=
,
即3x+y-1=0;
(2)由两点求斜率可得kBC=
=1,
∴BC边上的高线AE的斜率为-1,
∴AE所在直线方程为y-4=-1×(x+1),即x+y-3=0;
由B(-2,-1),C(2,3)可得BC边所在直线方程为
=
,
即x-y+1=0.
由A到BC的距离可得AE的长度为
=2
;
(3)由题意可知,当直线斜率不存在时,直线方程为x=-1,满足C到l的距离为3;
当直线斜率存在时,设直线方程为y-4=k(x+1),即kx-y+k+4=0.
由点到直线的距离公式得
=3,解得k=
.
∴直线方程为:4x-3y+16=0.
∴满足条件的直线方程为x=-1或4x-3y+16=0.
由中点坐标公式得D(0,1),
又A(-1,4),
∴BC边中线AD所在的直线方程为
| y-1 |
| 4-1 |
| x-0 |
| -1-0 |
即3x+y-1=0;
(2)由两点求斜率可得kBC=
| 3+1 |
| 2+2 |
∴BC边上的高线AE的斜率为-1,
∴AE所在直线方程为y-4=-1×(x+1),即x+y-3=0;
由B(-2,-1),C(2,3)可得BC边所在直线方程为
| y+1 |
| 3+1 |
| x+2 |
| 2+2 |
即x-y+1=0.
由A到BC的距离可得AE的长度为
| |-1-4+1| | ||
|
| 2 |
(3)由题意可知,当直线斜率不存在时,直线方程为x=-1,满足C到l的距离为3;
当直线斜率存在时,设直线方程为y-4=k(x+1),即kx-y+k+4=0.
由点到直线的距离公式得
| |2k-3+k+4| | ||
|
| 4 |
| 3 |
∴直线方程为:4x-3y+16=0.
∴满足条件的直线方程为x=-1或4x-3y+16=0.
点评:本题考查了直线的一般式方程和直线垂直的关系,考查了点到直线距离公式的应用,是基础的计算题.

练习册系列答案
 金钥匙试卷系列答案
金钥匙试卷系列答案
相关题目
函数f(x)=ln(1+x)+
的定义域为( )
| ||
| x |
| A、(-1,0)∪(0,1] |
| B、(-1,1) |
| C、(-1,1] |
| D、[-1,0)∪(0,1] |
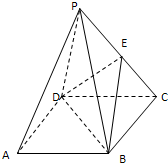 ,底面BCD是直角梯形,AB∥CD,∠ADC=90°,AB=AD=PD=1,CD=2.
,底面BCD是直角梯形,AB∥CD,∠ADC=90°,AB=AD=PD=1,CD=2.