题目内容
已知函数f（x）=2sin（2x+| π |
| 3 |
（1）在给定的直角坐标系中，运用“五点法”画出该函数在x∈[-
| π |
| 6 |
| 5π |
| 6 |
（2）若θ为锐角，且满足f（θ）-f（-θ）=1，求θ的值．
考点：五点法作函数y=Asin（ωx+φ）的图象,运用诱导公式化简求值
专题：三角函数的求值,三角函数的图像与性质
分析：（1）直接利用五点法，令2x+
=0，
，π，
，2π，列表求出对应的x即可找到五个特殊点的坐标，即可得到函数图象．
（2）由已知可解得sin2θ=
，根据角的范围，即可求θ的值．
| π |
| 3 |
| π |
| 2 |
| 3π |
| 2 |
（2）由已知可解得sin2θ=
| 1 |
| 2 |
解答：
解：（1）列表：…（2分）
描点，连线：得y=f（x）在一个周期内的图象．如右图所示（描5个点正确给（1分），图象基本正确给2分）．…（5分）
（2）∵θ为锐角，且满足f（θ）-f（-θ）=1，∴0＜2θ＜π，
∴f（θ）-f（-θ）=2sin（2θ+
）-2sin（-2θ+
）=sin2θ+
cos2θ+sin2θ-
cos2θ=2sin2θ=1，可解得sin2θ=
，
∴2θ=
或
．
∴θ=
或
．
| x | -
|
|
|
|
| ||||||||||
2x+
| 0 |
| π |
| 2π | ||||||||||
| f（x） | 0 | 2 | 0 | -2 | 0 |
（2）∵θ为锐角，且满足f（θ）-f（-θ）=1，∴0＜2θ＜π，
∴f（θ）-f（-θ）=2sin（2θ+
| π |
| 3 |
| π |
| 3 |
| 3 |
| 3 |
| 1 |
| 2 |
∴2θ=
| π |
| 6 |
| 5π |
| 6 |
∴θ=
| π |
| 12 |
| 5π |
| 12 |
点评：本题主要考查了五点法作函数y=Asin（ωx+φ）的图象，三角函数作图，要注意取关键点和端点，注意自变量的取值范围，属于基本知识的考查．
练习册系列答案
阅读快车系列答案
相关题目
已知椭圆C1：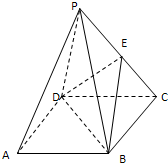
，底面BCD是直角梯形，AB∥CD，∠ADC=90°，AB=AD=PD=1，CD=2．