题目内容
已知数列{an}满足a1=1,a2n=a2n-1+(-1)n,a2n+1=a2n+3n(n∈N*),则数列{an}的前10项的和为 .
考点:数列的求和
专题:点列、递归数列与数学归纳法
分析:把a2n=a2n-1+(-1)n代入a2n+1=a2n+3n,得到a2n+1=a2n+3n=a2n-1+(-1)n+3n,依次取n为n-1,
n-2,…,1,类加后求得a2n-1,进一步得到a2n,则分组可求数列{an}的前10项的和.
n-2,…,1,类加后求得a2n-1,进一步得到a2n,则分组可求数列{an}的前10项的和.
解答:
解:由a1=1,a2n=a2n-1+(-1)n,a2n+1=a2n+3n(n∈N*),得
a2n+1=a2n+3n=a2n-1+(-1)n+3n,
a2n-1=a2n-3+(-1)n-1+3n-1,
a2n-3=a2n-5+(-1)n-2+3n-2,
…
a5=a3+(-1)2+32,
a3=a1+(-1)1+31,
累加得:a2n-1+a2n-3+…+a5+a3=a2n-3+a2n-5+…+a3+a1
+(-1)1+(-1)2+…+(-1)n-2+(-1)n-1+31+32+…+3n-2+3n-1,
∴a2n-1=a1+
+
=1-
+
•(-1)n-1+
•3n-1-
=
•(-1)n-1+
•3n-1-1.
∴a2n=a2n-1+(-1)n=
•3n-1-
•(-1)n-1-1.
则S10=(a1+a3+a5+a7+a9)+(a2+a4+a6+a8+a10)
=
[(-1)0+31-1+(-1)1+32-1+…+(-1)4+35-1]
+
[31-(-1)0-1+32-(-1)1-1+…+35-(-1)4-1]
=3+32+33+34+35-5
=
-5
=358.
故答案为:358.
a2n+1=a2n+3n=a2n-1+(-1)n+3n,
a2n-1=a2n-3+(-1)n-1+3n-1,
a2n-3=a2n-5+(-1)n-2+3n-2,
…
a5=a3+(-1)2+32,
a3=a1+(-1)1+31,
累加得:a2n-1+a2n-3+…+a5+a3=a2n-3+a2n-5+…+a3+a1
+(-1)1+(-1)2+…+(-1)n-2+(-1)n-1+31+32+…+3n-2+3n-1,
∴a2n-1=a1+
| -1[1-(-1)n-1] |
| 2 |
| 3(1-3n-1) |
| 1-3 |
=1-
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
∴a2n=a2n-1+(-1)n=
| 3 |
| 2 |
| 1 |
| 2 |
则S10=(a1+a3+a5+a7+a9)+(a2+a4+a6+a8+a10)
=
| 1 |
| 2 |
+
| 1 |
| 2 |
=3+32+33+34+35-5
=
| 3(1-35) |
| 1-3 |
=358.
故答案为:358.
点评:本题考查了数列递推式,考查了累加法求数列的通项公式,是中档题.

练习册系列答案
 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案
相关题目
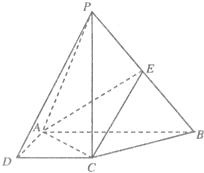 如图,在四棱锥P-ABCD中,底面ABCD是直角梯形,AB⊥AD,AB∥CD,AB=2AD=2CD=2,BC=
如图,在四棱锥P-ABCD中,底面ABCD是直角梯形,AB⊥AD,AB∥CD,AB=2AD=2CD=2,BC=