题目内容
对于函数f(x)=ex-e-x的叙述正确的是 .(填正确序号)
(1)f(x)为奇函数
(2)f(x)为增函数
(3)f(x)在x=0处取极值
(4)f(x)的图象关于点(0,1)对称.
(1)f(x)为奇函数
(2)f(x)为增函数
(3)f(x)在x=0处取极值
(4)f(x)的图象关于点(0,1)对称.
考点:利用导数研究函数的极值,函数单调性的判断与证明,函数奇偶性的判断
专题:计算题,函数的性质及应用,导数的综合应用
分析:由题意,f(x)的定义域为R,可求得f(-x)=-f(x),则f(x)为奇函数,故(1)正确,(4)不正确;
由ex是增函数,e-x是减函数,借助函数的四则运算知函数f(x)=ex-e-x是增函数,故(2)正确,(3)不正确.
由ex是增函数,e-x是减函数,借助函数的四则运算知函数f(x)=ex-e-x是增函数,故(2)正确,(3)不正确.
解答:
解:f(x)的定义域为R,
f(-x)=e-x-ex=-(ex-e-x)=-f(x),
则f(x)为奇函数,从而(1)正确;
∵ex是增函数,e-x是减函数,
∴函数f(x)=ex-e-x是增函数,
故(2)正确;
∵函数f(x)=ex-e-x是增函数,故f(x)在x=0处无极值;故(3)不正确;
由(1)知,f(x)的图象不可能关于点(0,1)对称,故(4)不正确;
故答案为:(1)(2).
f(-x)=e-x-ex=-(ex-e-x)=-f(x),
则f(x)为奇函数,从而(1)正确;
∵ex是增函数,e-x是减函数,
∴函数f(x)=ex-e-x是增函数,
故(2)正确;
∵函数f(x)=ex-e-x是增函数,故f(x)在x=0处无极值;故(3)不正确;
由(1)知,f(x)的图象不可能关于点(0,1)对称,故(4)不正确;
故答案为:(1)(2).
点评:本题考查了函数的奇偶性的判断,及通过函数的导数求函数的单调性及极值的步骤,属于中档题.

练习册系列答案
相关题目
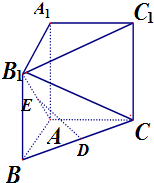 在三棱柱ABC-A1B1C1中,侧棱AA1⊥底面ABC,AB=AC=1,∠BAC=120°,异面直线B1C与AA1成60°角,D,E分别是BC,AB1的中点.
在三棱柱ABC-A1B1C1中,侧棱AA1⊥底面ABC,AB=AC=1,∠BAC=120°,异面直线B1C与AA1成60°角,D,E分别是BC,AB1的中点.