题目内容
设f(x)是R上的偶函数,且当x≥0时,f(x)=2x-2x
;函数g(x)=ln(x+1)-
.则:
(1)函数g(x)的零点个数为 ;
(2)若实数a是函数g(x)的正零点,则f(-2)与f(a)的大小关系为 .
| 1 |
| 2 |
| 2 |
| x |
(1)函数g(x)的零点个数为
(2)若实数a是函数g(x)的正零点,则f(-2)与f(a)的大小关系为
考点:函数奇偶性的性质
专题:函数的性质及应用
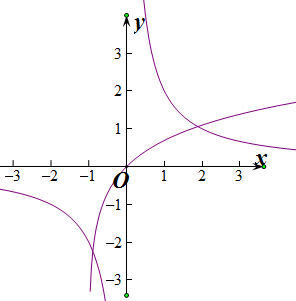
分析:(1)分别画出分别画出y=ln(x+1)和y=
的图象,由图象可知,函数g(x)的零点个数为2个;
(2)由图象可知a∈(1,2);再根据函数为偶函数,得到f(-2)=f(2),以及利用导数得到函数在(1,+∞)为增函数,问题得以解决.
| 2 |
| x |
(2)由图象可知a∈(1,2);再根据函数为偶函数,得到f(-2)=f(2),以及利用导数得到函数在(1,+∞)为增函数,问题得以解决.
解答:
 解:(1)∵g(x)=ln(x+1)-
解:(1)∵g(x)=ln(x+1)-
,
∴g(x)=ln(x+1)-
=0,
即ln(x+1)=
,
分别画出y=ln(x+1)和y=
的图象,
由图象可知,函数g(x)的零点个数为2个;
(2),函数g(x)的2个零点,其一在(-1,0)上,另一在(1,2)上,
∵实数a是函数g(x)的正零点,
∴a∈(1,2);
对于f(x),在x≥0时,f(x)=2x-2x
,
∴f′(x)=2xln2-
,
当x>1时,f'(1)>2ln2-1>0,
∴f(x)在(1,+∞)上单调递增,
∴f(a)<f(2),
又函数f(x)为偶函数,
∴f(-2)=f(2)
∴f(a)<f(-2).
故答案为(1)2,(2)f(a)<f(-2)
 解:(1)∵g(x)=ln(x+1)-
解:(1)∵g(x)=ln(x+1)-| 2 |
| x |
∴g(x)=ln(x+1)-
| 2 |
| x |
即ln(x+1)=
| 2 |
| x |
分别画出y=ln(x+1)和y=
| 2 |
| x |
由图象可知,函数g(x)的零点个数为2个;
(2),函数g(x)的2个零点,其一在(-1,0)上,另一在(1,2)上,
∵实数a是函数g(x)的正零点,
∴a∈(1,2);
对于f(x),在x≥0时,f(x)=2x-2x
| 1 |
| 2 |
∴f′(x)=2xln2-
| 1 | ||
|
当x>1时,f'(1)>2ln2-1>0,
∴f(x)在(1,+∞)上单调递增,
∴f(a)<f(2),
又函数f(x)为偶函数,
∴f(-2)=f(2)
∴f(a)<f(-2).
故答案为(1)2,(2)f(a)<f(-2)
点评:本题主要考查了函数的零点问题以及函数的奇偶性和函数的单调性,以及数形结合的思想,属于中档题.

练习册系列答案
相关题目
设集合A={x|1<x≤2},B={ x|x<a},若A⊆B,则a的取值范围是( )
| A、{a|a≥1} |
| B、{a|a≤1} |
| C、{a|a≥2} |
| D、{a|a>2} |
若不等式组
表示的平面区域不能构成三角形,则a的范围是( )
|
A、1<a<
| ||
B、1<a≤
| ||
C、1≤a≤
| ||
D、1≤a<
|
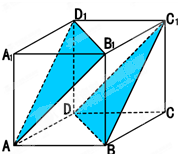 已知正方体ABCD-A1B1C1D1.求证:
已知正方体ABCD-A1B1C1D1.求证: