题目内容
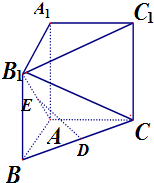在三棱柱ABC-A1B1C1中，侧棱AA1⊥底面ABC，AB=AC=1，∠BAC=120°，异面直线B1C与AA1成60°角，D，E分别是BC，AB1的中点．（1）求证：DE∥平面AA1C1C．
（2）求三棱锥B1-ABC的体积．
考点：直线与平面平行的判定,棱柱、棱锥、棱台的体积
专题：空间位置关系与距离,空间角
分析：（1）首先连结 A1B，A1C在三棱柱ABC-A1B1C1中，侧面是平行四边形，D，E分别是BC，AB1的中点，所以DE∥A1C，DE?平面AA1C1C，A1C?平面AA1C1C，DE∥平面AA1C1C
（2）异面直线B1C与AA1成60°角，所以∠CB1B=60°，侧棱AA1⊥底面ABC，侧棱BB1⊥底面ABC利用三角函数求得：BB1=1，AB=AC=1，∠BAC=120°，进一步求出底面的面积，和锥体的体积．
（2）异面直线B1C与AA1成60°角，所以∠CB1B=60°，侧棱AA1⊥底面ABC，侧棱BB1⊥底面ABC利用三角函数求得：BB1=1，AB=AC=1，∠BAC=120°，进一步求出底面的面积，和锥体的体积．
解答：
（1）证明：连结 A1B，A1C在三棱柱ABC-A1B1C1中，侧面是平行四边形
D，E分别是BC，AB1的中点
所以DE∥A1C
DE?平面AA1C1C，A1C?平面AA1C1C
DE∥平面AA1C1C
（2）异面直线B1C与AA1成60°角
所以∠CB1B=60°
侧棱AA1⊥底面ABC
侧棱BB1⊥底面ABC
利用三角函数求得：BB1=1
AB=AC=1，∠BAC=120°
S△ABC=
•1•1•sin120°=
VB1-ABC=
•1•
=
D，E分别是BC，AB1的中点
所以DE∥A1C
DE?平面AA1C1C，A1C?平面AA1C1C
DE∥平面AA1C1C
（2）异面直线B1C与AA1成60°角
所以∠CB1B=60°
侧棱AA1⊥底面ABC
侧棱BB1⊥底面ABC
利用三角函数求得：BB1=1
AB=AC=1，∠BAC=120°
S△ABC=
| 1 |
| 2 |
| ||
| 4 |
VB1-ABC=
| 1 |
| 3 |
| ||
| 4 |
| ||
| 12 |
点评：本题考查的知识要点：三角形中位线定理，线面平行的判定定理，三角形的面积公式，锥体的体积公式，异面直线的夹角．
练习册系列答案
快乐暑假暑假能力自测中西书局系列答案
相关题目
已知三条直线a，b，c，两个平面α，β．则下列命题中：
①a∥c，c∥b⇒a∥b；
②若m⊥α，m∥n，n?β⇒α⊥β；
③a∥c，c∥α⇒a∥α；
④α∥β，a∥α⇒∥β；
⑤a?α，b∥a，a∥b⇒α∥a，
正确的命题是（ ）
①a∥c，c∥b⇒a∥b；
②若m⊥α，m∥n，n?β⇒α⊥β；
③a∥c，c∥α⇒a∥α；
④α∥β，a∥α⇒∥β；
⑤a?α，b∥a，a∥b⇒α∥a，
正确的命题是（ ）
| A、②④ | B、①② | C、①②⑤ | D、③⑤ |
设集合A={x|1＜x≤2}，B={ x|x＜a}，若A⊆B，则a的取值范围是（ ）
| A、{a|a≥1} |
| B、{a|a≤1} |
| C、{a|a≥2} |
| D、{a|a＞2} |
已知正方体ABCD-A1B1C1D1．求证：定义在R上的函数f（x）满足xf′（x）≤0，且y=f（x）为偶函数，当|x1|＜|x2|时，有（ ）
| A、f（x1）＞f（x2） |
| B、f（x1）=f（x2） |
| C、f（x1）＜f（x2） |
| D、f（|x2|）＞f（x1） |