题目内容

1．如图，一个空间几何体的三视图中，正视图和侧视图都是腰长为5，底边长为8的等腰三角形，俯视图为边长为8的正方形，则该几何体的体积为（　　）
A．192B．32C．320D．64

分析 由三视图得出该几何体是底面为正方形的四棱锥，求出棱锥的高，计算四棱锥的体积．

解答 解：由三视图可知，该几何体为四棱锥，如图所示；
底面为正方形边长为8，棱锥的高PO=$\sqrt{{5}^{2}{-4}^{2}}$=3，
∴四棱锥的体积为V=$\frac{1}{3}$•82•3=64．
故选：D．

点评 本题考查了由几何体的三视图求几何体的体积，利用三视图还原成空间几何体的直观图，是解题的关键．

练习册系列答案
相关题目
8．已知点P（x，y）是曲线C上任意一点，点（x，2y）在圆x2+y2=8上，定点M（2，1），平行于OM的直线l在y轴上的截距为m（m≠0），直线l与曲线C交于A、B两个不同点．
（1）求曲线C的方程；
（2）求证直线MA、MB与x轴始终围成一个等腰三角形．
12．已知曲线C1的方程为x2+y2=1，过平面上一点P1作C1的两条切线，切点分别为A1，B1，且满足∠A1P1B1=$\frac{π}{3}$，记P1的轨迹为C2，过一点P2作C2的两条切线，切点分别为A2，B2满足∠A2P2B2=$\frac{π}{3}$，记P2的轨迹为C3，按上述规律一直进行下去…，记an=|AnAn+1|max且Sn为数列{$\frac{1}{{a}_{n}}$}的前n项和，则满足|Sn-$\frac{2}{3}$|＜$\frac{1}{100}$的最小的n是7．
9．已知点A，B，C在圆x2+y2=4上运动，且AB⊥BC．若点P的坐标为（3，4），则$|{\overrightarrow{PA}+\overrightarrow{PB}+\overrightarrow{PC}}|$的取值范围为（　　）
A．[10，15]B．[12，17]C．[13，17]D．[15，17]
16．一个四棱锥的侧棱长都相等，底面是正方形，且其正视图为如图所示的等腰三角形，则该四棱锥的表面积是（　　）
A．12B．$4\sqrt{5}$C．$4+4\sqrt{3}$D．$4+4\sqrt{5}$
6．2017年5月14日至15日，中国在北京举办“一带一路”国际合作高峰论坛，与其它60多个成员国共商大计．设S是由不少于4个成员国代表组成的集合，如果S中任意4个代表都至少有1个人与另外3个人认识，那么下列判定正确的是（　　）
A．S中没有人认识S中所有的人B．S中至少有1人认识S中所有的人
C．S中至多有2人不认识S中所有的人D．S中至多有2人认识S中所有的人
13．观察下列等式：

可以推测：13+23+33+…+n3=3025时，n=10（n∈N*）．
10．设函数f（x）=|2x+2|+|2x-3|．
（1）求不等式f（x）＞7 的解集；
（2）若关于x的不等式f（x）≤|3m-2|有解，求实数m的取值范围．
11．正整数按如表的规律排列，则第2017行，第2016列的数应为（　　）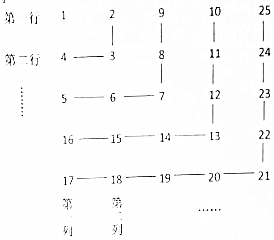
A．20162B．2016×2017C．20172D．2017×2018

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网