题目内容
9.已知点A,B,C在圆x2+y2=4上运动,且AB⊥BC.若点P的坐标为(3,4),则$|{\overrightarrow{PA}+\overrightarrow{PB}+\overrightarrow{PC}}|$的取值范围为( )| A. | [10,15] | B. | [12,17] | C. | [13,17] | D. | [15,17] |
分析 画出图形,由题意可知AC为圆的直径,设出B,利用向量坐标加法运算求得$\overrightarrow{PA}+\overrightarrow{PB}+\overrightarrow{PC}$的坐标,再求模,利用三角函数求最值.
解答 解:∵AB⊥BC,∴AC为圆x2+y2=4的直径,如图,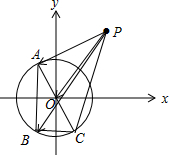
∵P(3,4),∴$\overrightarrow{PA}+\overrightarrow{PC}=2\overrightarrow{PO}=(-6,-8)$,
设B(2cosθ,2sinθ),则$\overrightarrow{PB}=(2cosθ-3,2sinθ-4)$.
∴$|{\overrightarrow{PA}+\overrightarrow{PB}+\overrightarrow{PC}}|$=|(2cosθ-9,2sinθ-12)|=$\sqrt{(2cosθ-9)^{2}+(2sinθ-12)^{2}}$
=$\sqrt{229-12(4sinθ+3cosθ)}$=$\sqrt{229-60sin(θ+α)}$(tanα=$\frac{3}{4}$).
∴$|{\overrightarrow{PA}+\overrightarrow{PB}+\overrightarrow{PC}}|$的最小值为$\sqrt{229-60}=13$,最大值为$\sqrt{229+60}=17$.
∴$|{\overrightarrow{PA}+\overrightarrow{PB}+\overrightarrow{PC}}|$的取值范围为[13,17].
故选:C.
点评 本题考查平面向量的数量积运算,考查了三角函数最值的求法,考查直线与圆的位置关系的应用,是中档题.

练习册系列答案
相关题目
4.老师带甲乙丙丁四名学生去参加自主招生考试,考试结束后老师向四名学生了解考试情况,四名学生的回答如下:
甲说:“我们四人都没考好”;
乙说:“我们四人中有人考得好”;
丙说:“乙和丁至少有一人没考好”;
丁说:“我没考好”.
成绩出来后发现,四名学生中有且只有两人说对了,他们是( )
甲说:“我们四人都没考好”;
乙说:“我们四人中有人考得好”;
丙说:“乙和丁至少有一人没考好”;
丁说:“我没考好”.
成绩出来后发现,四名学生中有且只有两人说对了,他们是( )
| A. | 甲、丙 | B. | 乙、丁 | C. | 丙、丁 | D. | 乙、丙 |
1. 如图,一个空间几何体的三视图中,正视图和侧视图都是腰长为5,底边长为8的等腰三角形,俯视图为边长为8的正方形,则该几何体的体积为( )
如图,一个空间几何体的三视图中,正视图和侧视图都是腰长为5,底边长为8的等腰三角形,俯视图为边长为8的正方形,则该几何体的体积为( )
 如图,一个空间几何体的三视图中,正视图和侧视图都是腰长为5,底边长为8的等腰三角形,俯视图为边长为8的正方形,则该几何体的体积为( )
如图,一个空间几何体的三视图中,正视图和侧视图都是腰长为5,底边长为8的等腰三角形,俯视图为边长为8的正方形,则该几何体的体积为( )| A. | 192 | B. | 32 | C. | 320 | D. | 64 |
 我国的《洛书》中记载着世界上最古老的幻方:将1,2,…,9填入方格内,使三行、三列,两条对角线的三个数之和都等于15,如图所示.
我国的《洛书》中记载着世界上最古老的幻方:将1,2,…,9填入方格内,使三行、三列,两条对角线的三个数之和都等于15,如图所示. 如图,正四棱锥 (底面是正方形,顶点在底面的射影是底面的中心) P-ABCD的底面边长为6cm,侧棱长为5cm,正方形ABCD的中心为O,PO⊥OA,则它的侧视图的面积等于3$\sqrt{7}$ cm.
如图,正四棱锥 (底面是正方形,顶点在底面的射影是底面的中心) P-ABCD的底面边长为6cm,侧棱长为5cm,正方形ABCD的中心为O,PO⊥OA,则它的侧视图的面积等于3$\sqrt{7}$ cm.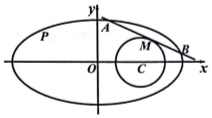 已知椭圆方程为$\frac{{x}^{2}}{4}$+y2=1,圆C:(x-1)2+y2=r2.
已知椭圆方程为$\frac{{x}^{2}}{4}$+y2=1,圆C:(x-1)2+y2=r2.