题目内容
(1)已知{an}是公比为q的等比数列,且a1,a3,a2成等差数列.求q的值;
(2)设数列{an}的前n项和为Sn,已知Sn=
,求数列{an}的通项公式.
(2)设数列{an}的前n项和为Sn,已知Sn=
| n2+3n |
| 2 |
考点:数列的求和,等比数列的性质
专题:等差数列与等比数列
分析:(1)直接由a1,a3,a2成等差数列列式求得q的值;
(2)当n=1时,直接由前n项和求首项,当n≥2时,由an=Sn-Sn-1求通项,验证首项后得答案.
(2)当n=1时,直接由前n项和求首项,当n≥2时,由an=Sn-Sn-1求通项,验证首项后得答案.
解答:
解:(1)由a1,a3,a2成等差数列,得
2a1q2=a1+a1q,即2q2-q-1=0,解得q=1或q=-
;
(2)由Sn=
,得a1=2.
当n≥2时,an=Sn-Sn-1=
-
=n+1.
验证n=1上式成立.
∴an=n+1.
2a1q2=a1+a1q,即2q2-q-1=0,解得q=1或q=-
| 1 |
| 2 |
(2)由Sn=
| n2+3n |
| 2 |
当n≥2时,an=Sn-Sn-1=
| n2+3n |
| 2 |
| (n-1)2+3(n-1) |
| 2 |
验证n=1上式成立.
∴an=n+1.
点评:本题考查了等比数列的通项公式和等差数列的性质,考查了由数列的和求通项公式,是中档题.

练习册系列答案
相关题目
 已知函数f(x)=sin2x+2sin(
已知函数f(x)=sin2x+2sin(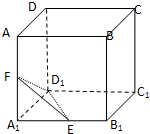 如图,在正方体ABCD-A1B1C1D1中,E,F分别为棱A1B1,A1A的中点.
如图,在正方体ABCD-A1B1C1D1中,E,F分别为棱A1B1,A1A的中点.