题目内容
(1)已知函数f(x)=ax+b,f(1)=5,f(-3)=-3,求f(x)
(2)已知函数f(x)与g(x)分别由下表给出:
用分段函数表示y=f[g(x)],并画出函数y=f[g(x)]的图象.
(2)已知函数f(x)与g(x)分别由下表给出:
| x | 1 | 2 |
| f(x) | 3 | 6 |
| x | 1 | 2 |
| g(x) | 2 | 1 |
考点:分段函数的应用,函数的值
专题:计算题,函数的性质及应用
分析:(1)由条件得到a,b的方程组,解出即可;
(2)由图表,求出x=1、x=2的函数值,即可,并画出图象,注意是孤立的点.
(2)由图表,求出x=1、x=2的函数值,即可,并画出图象,注意是孤立的点.
解答:
 解:(1)∵f(1)=5,f(-3)=-3,
解:(1)∵f(1)=5,f(-3)=-3,
∴
,
则
,
∴f(x)=2x+3;
(2)f[g(x)]=
,
函数y=f[g(x)]的图象如图所示.
 解:(1)∵f(1)=5,f(-3)=-3,
解:(1)∵f(1)=5,f(-3)=-3,∴
|
则
|
∴f(x)=2x+3;
(2)f[g(x)]=
|
函数y=f[g(x)]的图象如图所示.
点评:本题考查分段函数及运用,考查函数的解析式的求法,以及分段函数的图象,属于基础题.

练习册系列答案
相关题目

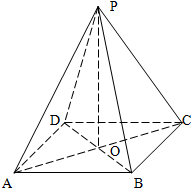 如图,四棱锥P-ABCD的侧棱都相等,底面ABCD是正方形,O为对角线AC、BD的交点,PO=OA.
如图,四棱锥P-ABCD的侧棱都相等,底面ABCD是正方形,O为对角线AC、BD的交点,PO=OA.