题目内容
已知函数f(x)=lg(x2+tx+1),(t为常数,且t>-2)
(1)当t=2时,求函数f(x)的定义域;
(2)当x∈[0,2]时,求f(x)的最小值(用t表示);
(3)是否存在不同的实数a,b,使得f(a)=lga,f(b)=lgb,并且a,b∈(0,2),若存在,求出实数t的取值范围;若不存在,请说明理由.
(1)当t=2时,求函数f(x)的定义域;
(2)当x∈[0,2]时,求f(x)的最小值(用t表示);
(3)是否存在不同的实数a,b,使得f(a)=lga,f(b)=lgb,并且a,b∈(0,2),若存在,求出实数t的取值范围;若不存在,请说明理由.
考点:抽象函数及其应用,函数的定义域及其求法
专题:计算题,存在型,数形结合,分类讨论,函数的性质及应用
分析:(1)由x2+2x+1>0即可得到f(x)的定义域为{x|x≠-1,且x∈R};
(2)令g(x)=x2+tx+1,要求函数f(x)的最小值,根据复合函数的单调性可知,只要求解函数g(x)的最小值即可,结合图象,需判断对称轴与区间[0,2]的位置关系,分类讨论①-
≤0②0<-
<2③-
≥2;
(3)假设存在,则由已知得
等价于x2+tx+1=x在区间(0,2)上有两个不同的实根,
分离参数,得t=-(
+x)+1,x∈(0,2),运用导数求出右边的最值和范围,结合图象即可判断.
(2)令g(x)=x2+tx+1,要求函数f(x)的最小值,根据复合函数的单调性可知,只要求解函数g(x)的最小值即可,结合图象,需判断对称轴与区间[0,2]的位置关系,分类讨论①-
| t |
| 2 |
| t |
| 2 |
| t |
| 2 |
(3)假设存在,则由已知得
|
分离参数,得t=-(
| 1 |
| x |
解答:
解:(1)当t=2时,f(x)=lg(x2+2x+1),
x2+2x+1>0⇒f(x)的定义域为{x|x≠-1,且x∈R};
(2)令g(x)=x2+tx+1对称轴为x=-
,
①当-
≤0,即t≥0时,g(x)min=g(0)=1∴f(x)min=0
②当0<-
<2,即-4<t<0时,g(x)min=g(-
)=1-
,考虑到g(x)>0,则
1°-2<t<0,f(x)min=f(-
)=lg(1-
),
2°-4<t≤-2,没有最小值.
③当-
≥2,即t≤-4时,g(x)min=g(2)=5+2t,
考虑到g(x)>0∴f(x)没有最小值.
综上所述:当t≤-2时f(x)没有最小值;
当t>-2时f(x)=
.
(3)假设存在,则由已知得
等价于x2+tx+1=x在区间(0,2)上有两个不同的实根,
等价于t=-(
+x)+1,x∈(0,2),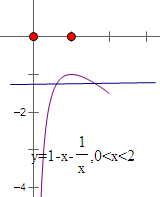
t′=-1+
,x∈(0,1),t′>0;x∈(1,2),t′<0.
x=1取最大值-1.x=2,t=-
.
可得-
<t<-1.
故存在,实数t的取值范围是(-
,-1).
x2+2x+1>0⇒f(x)的定义域为{x|x≠-1,且x∈R};
(2)令g(x)=x2+tx+1对称轴为x=-
| t |
| 2 |
①当-
| t |
| 2 |
②当0<-
| t |
| 2 |
| t |
| 2 |
| t2 |
| 4 |
1°-2<t<0,f(x)min=f(-
| t |
| 2 |
| t2 |
| 4 |
2°-4<t≤-2,没有最小值.
③当-
| t |
| 2 |
考虑到g(x)>0∴f(x)没有最小值.
综上所述:当t≤-2时f(x)没有最小值;
当t>-2时f(x)=
|
(3)假设存在,则由已知得
|
等价于t=-(
| 1 |
| x |

t′=-1+
| 1 |
| x2 |
x=1取最大值-1.x=2,t=-
| 3 |
| 2 |
可得-
| 3 |
| 2 |
故存在,实数t的取值范围是(-
| 3 |
| 2 |
点评:本题主要考查了对数函数定义域的求解,复合函数单调性的应用及二次函数在闭区间上的最值的求解,要注意考虑对称轴与区间位置关系的讨论,二次方程的实根分布问题的应用,本题的综合性比较强.

练习册系列答案
相关题目
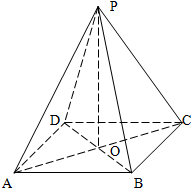 如图,四棱锥P-ABCD的侧棱都相等,底面ABCD是正方形,O为对角线AC、BD的交点,PO=OA.
如图,四棱锥P-ABCD的侧棱都相等,底面ABCD是正方形,O为对角线AC、BD的交点,PO=OA.