题目内容
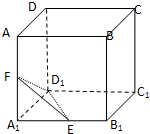 如图,在正方体ABCD-A1B1C1D1中,E,F分别为棱A1B1,A1A的中点.
如图,在正方体ABCD-A1B1C1D1中,E,F分别为棱A1B1,A1A的中点.(Ⅰ)判定D,C1,E,F是否在同一平面上?若在同一平面上,请加以证明,若不在同一平面上,请说明理由;
(Ⅱ)已知正方体的棱长为2,沿平面EFD1截去三棱锥A1-EFD1;
(i)求余下几何体的体积;
(ii)求余下几何体的表面积.
考点:棱柱、棱锥、棱台的体积,棱柱、棱锥、棱台的侧面积和表面积,平面的基本性质及推论
专题:综合题,空间位置关系与距离
分析:(Ⅰ)证明EF∥DC1,可得D,C1,E,F四点在同一个平面上;
(Ⅱ)(i)求出三棱锥A1-EFD1的体积,即可求余下几何体的体积;
(ii)求出△D1EF的面积,即可求余下几何体的表面积.
(Ⅱ)(i)求出三棱锥A1-EFD1的体积,即可求余下几何体的体积;
(ii)求出△D1EF的面积,即可求余下几何体的表面积.
解答:
解:(I)答:D,C1,E,F四点在同一个平面上…(1分)
证明:连结AB1,由E,F分别为棱A1B1,A1A的中点,所以EF∥AB1,
又由正方体知AB1∥DC1,
由平行公理得EF∥DC1,因此,D,C1,E,F四点在同一个平面上…(4分)
(II)(i)由三棱锥A1-EFD1的体积V1=
(
×1×1)×2=
…(6分)
所以,余下几何体的体积V=V正方体-V1=23-
=
…(8分)
(ii)依题意可得D1F=D1E=
,在△D1EF中,过D1作D1H垂直于EF,垂足为H,则D1H=
=
,所以△D1EF的面积S△D1EF=
×
×
=
…(10分)
余下几何体的表面积S=.3×22+(3×22-1-1-
)+
=23…(12分)
证明:连结AB1,由E,F分别为棱A1B1,A1A的中点,所以EF∥AB1,
又由正方体知AB1∥DC1,
由平行公理得EF∥DC1,因此,D,C1,E,F四点在同一个平面上…(4分)
(II)(i)由三棱锥A1-EFD1的体积V1=
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 3 |
所以,余下几何体的体积V=V正方体-V1=23-
| 1 |
| 3 |
| 23 |
| 3 |
(ii)依题意可得D1F=D1E=
| 5 |
5-
|
3
| ||
| 2 |
| 1 |
| 2 |
| 2 |
3
| ||
| 2 |
| 3 |
| 2 |
余下几何体的表面积S=.3×22+(3×22-1-1-
| 1 |
| 2 |
| 3 |
| 2 |
点评:本题考查棱柱、棱锥、棱台的侧面积和表面积、体积,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
相关题目