题目内容
 已知函数f(x)=sin2x+2sin(
已知函数f(x)=sin2x+2sin(| π |
| 4 |
| π |
| 4 |
(1)求函数f(x)的最小正周期;
(2)求函数f(x)在区间[-
| π |
| 12 |
| π |
| 2 |
(3)借助”五点作图法”画出函数f(x)在[0,
| 7π |
| 8 |
| 7π |
| 8 |
考点:两角和与差的正弦函数,正弦函数的定义域和值域,五点法作函数y=Asin(ωx+φ)的图象
专题:三角函数的图像与性质
分析:(1)根据诱导公式、两角和的正弦函数公式化简解析式,再求出函数的周期;
(2)由x的范围求出2x+
∈[
,
],根据正弦函数的性质求出函数的最小值、最大值,即可求出函数的值域;
(3)由条件列出表格、再描点连线画出函数的图象,根据图象写出递增区间.
(2)由x的范围求出2x+
| π |
| 4 |
| π |
| 12 |
| 5π |
| 4 |
(3)由条件列出表格、再描点连线画出函数的图象,根据图象写出递增区间.
解答:
解:(1)∵f (x)=sin 2x+sin (
-2x)
=sin 2x+cos2x
=
(
sin 2x+
cos 2x)
=
(sin 2x cos
+cos 2x sin
)
=
sin (2x+
)
∴函数的周期T=
=π …(4分)
(2)∵x∈[-
,
],∴2x+
∈[
,
],
当2x+
=
时,f(x)取最大值
,
当2x+
=
时,f(x)取最小值
sin
=-1,
∴函数f(x)在区间[-
,
]上的值域为[-1,
]…(8分)
(3)列表
…(10分)
图象如右图所示,注意f(0)=1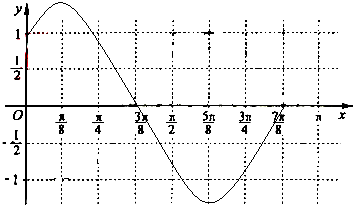 …(12分)
…(12分)
由图得,
函数在区间[0,
]上的单调递增区间是[0,
],[
,
]…(14分)
| π |
| 2 |
=sin 2x+cos2x
=
| 2 |
| ||
| 2 |
| ||
| 2 |
=
| 2 |
| π |
| 4 |
| π |
| 4 |
=
| 2 |
| π |
| 4 |
∴函数的周期T=
| 2π |
| 2 |
(2)∵x∈[-
| π |
| 12 |
| π |
| 2 |
| π |
| 4 |
| π |
| 12 |
| 5π |
| 4 |
当2x+
| π |
| 4 |
| π |
| 2 |
| 2 |
当2x+
| π |
| 4 |
| 5π |
| 4 |
| 2 |
| 5π |
| 4 |
∴函数f(x)在区间[-
| π |
| 12 |
| π |
| 2 |
| 2 |
(3)列表
μ=2x+
|
|
| π |
| 2π | ||||||||
| x | 0 |
|
|
|
| ||||||||
| y | 1 |
| 0 | -
| 0 |
图象如右图所示,注意f(0)=1
 …(12分)
…(12分)由图得,
函数在区间[0,
| 7π |
| 8 |
| π |
| 8 |
| 5π |
| 8 |
| 7π |
| 8 |
点评:本题考查诱导公式、两角和的正弦函数公式,正弦函数的图象与性质,以及五点作图法,属于中档题.

练习册系列答案
 学业测评一课一测系列答案
学业测评一课一测系列答案
相关题目
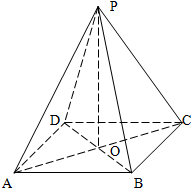 如图,四棱锥P-ABCD的侧棱都相等,底面ABCD是正方形,O为对角线AC、BD的交点,PO=OA.
如图,四棱锥P-ABCD的侧棱都相等,底面ABCD是正方形,O为对角线AC、BD的交点,PO=OA.