题目内容
已知椭圆
+
=1(a>b>0)上的点 (
,
)到它的两个焦点的距离之和为4
(Ⅰ)求椭圆的方程:
(Ⅱ)A,B是椭圆上关于x轴对称的两点,设D(4,0),连接DB交椭圆于另一点F,证明直线AE恒过x轴上的定点P;
(Ⅲ)在(Ⅱ)的条件下,过点P的直线与椭圆交于M,N两点,求
•
的取值范围.
| x2 |
| a2 |
| y2 |
| b2 |
| 3 |
| ||
| 2 |
(Ⅰ)求椭圆的方程:
(Ⅱ)A,B是椭圆上关于x轴对称的两点,设D(4,0),连接DB交椭圆于另一点F,证明直线AE恒过x轴上的定点P;
(Ⅲ)在(Ⅱ)的条件下,过点P的直线与椭圆交于M,N两点,求
| OM |
| ON |
考点:直线与圆锥曲线的综合问题
专题:圆锥曲线中的最值与范围问题
分析:(Ⅰ)由已知条件推导出
,由此能求出椭圆方程.
(Ⅱ)设直线BD的方程为y=k(x-4),联立方程组
,得(4k2+3)x2-32k2x+64k2-12=0,设点B(x1,y1),E(x2,y2),则A(x1,-y1),由已知条件推导出x=1.由此能证明直线AE恒过x轴上的定点P.
(Ⅲ)当过P点的直线MN的斜率存在时,设直线MN的方程为y=m(x-1),且M(xM,yM),N(xN,yN)在椭圆上,推导出
•
∈[-4,-
),当过P点的直线MN的斜率不存在时,
•
=-
,由此能求出
•
的取值范围.
|
(Ⅱ)设直线BD的方程为y=k(x-4),联立方程组
|
(Ⅲ)当过P点的直线MN的斜率存在时,设直线MN的方程为y=m(x-1),且M(xM,yM),N(xN,yN)在椭圆上,推导出
| OM |
| ON |
| 5 |
| 4 |
| OM |
| ON |
| 5 |
| 4 |
| OM |
| ON |
解答:
(Ⅰ)解:∵椭圆
+
=1(a>b>0)上的点 (
,
)到它的两个焦点的距离之和为4,
∴
,
解得a=2,b=
,
∴椭圆方程为
+
=1.
(Ⅱ)证明:由题意知BD的斜率存在,设直线BD的方程为y=k(x-4),
联立方程组
,得(4k2+3)x2-32k2x+64k2-12=0,①
设点B(x1,y1),E(x2,y2),则A(x1,-y1),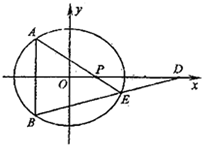
直线AE的方程为y-y2=
(x-x2)
(x-x2),
令y=0,得x=x2-
,
将y1=k(x1-4),y2=k(x2-4)代入上式,
整理,得x=
,②
由①得x1+x2=
,x1x2=
,将其代入②,
整理,得x=1.
∴直线AE与x轴相交于P(1,0),即直线AE恒过x轴上的定点P.
(Ⅲ)当过P点的直线MN的斜率存在时,
设直线MN的方程为y=m(x-1),且M(xM,yM),N(xN,yN)在椭圆上,
由
+
=1,y=m(x-1),得(4m2+3)x2-8m2x+4m2-12=0,
△=64m4-4(4m2+3)(4m2-12)=144m2+144>0,
∴xM+xN=
,xM•xN=
,yMyN=-
,
则
•
=xMxN+yMyN=-
=-
-
,
∵m2≥0,∴-
≤
<0,
∴
•
∈[-4,-
),
当过P点的直线MN的斜率不存在时,
直线MN的方程为x=1,M(1,
),N(1,-
),
此时
•
=-
,
∴
•
的取值范围是[-4,-
].
| x2 |
| a2 |
| y2 |
| b2 |
| 3 |
| ||
| 2 |
∴
|
解得a=2,b=
| 3 |
∴椭圆方程为
| x2 |
| 4 |
| y2 |
| 3 |
(Ⅱ)证明:由题意知BD的斜率存在,设直线BD的方程为y=k(x-4),
联立方程组
|
设点B(x1,y1),E(x2,y2),则A(x1,-y1),

直线AE的方程为y-y2=
| y2+y1 |
| x2-x1 |
| y2-y1 |
| x2-x1 |
令y=0,得x=x2-
| y2(x2-x1) |
| y2+y1 |
将y1=k(x1-4),y2=k(x2-4)代入上式,
整理,得x=
| 2x1x2-4(x1+x2) |
| x1+x2-8 |
由①得x1+x2=
| 32k2 |
| 4k2+3 |
| 64k2-12 |
| 4k2+3 |
整理,得x=1.
∴直线AE与x轴相交于P(1,0),即直线AE恒过x轴上的定点P.
(Ⅲ)当过P点的直线MN的斜率存在时,
设直线MN的方程为y=m(x-1),且M(xM,yM),N(xN,yN)在椭圆上,
由
| x2 |
| 4 |
| y2 |
| 3 |
△=64m4-4(4m2+3)(4m2-12)=144m2+144>0,
∴xM+xN=
| 8m2 |
| 4m2+3 |
| 4m2-12 |
| 4m2+3 |
| 9m2 |
| 4m2+3 |
则
| OM |
| ON |
| 5m2+12 |
| 4m2+3 |
| 5 |
| 4 |
| 33 |
| 4(4m2+3) |
∵m2≥0,∴-
| 11 |
| 4 |
| 33 |
| 4(4m2+3) |
∴
| OM |
| ON |
| 5 |
| 4 |
当过P点的直线MN的斜率不存在时,
直线MN的方程为x=1,M(1,
| 3 |
| 2 |
| 3 |
| 2 |
此时
| OM |
| ON |
| 5 |
| 4 |
∴
| OM |
| ON |
| 5 |
| 4 |
点评:本题考查椭圆方程的求法,考查直线恒过x轴上的定点,考查向量的数量积的取值范围的求法,解题时要认真审题,注意函数与方程思想的合理运用.

练习册系列答案
 活力试卷系列答案
活力试卷系列答案 课课优能力培优100分系列答案
课课优能力培优100分系列答案
相关题目
已知集合M={x|1<x<a},N={x|1<x<3},则“a=3”是“M⊆N”的( )
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
已知实数a,b满足|a-2|=
+
,则不等式2|1-a|-1>a(a-2)成立的概率为( )
| 3b+6 |
| 7-b |
A、
| ||
B、
| ||
C、
| ||
D、
|
复数
•i2014(i是虚数单位)为纯虚数,则实数a的值为( )
| 2a+i |
| 1-2i |
A、
| ||
B、-
| ||
| C、1 | ||
| D、-1 |