题目内容
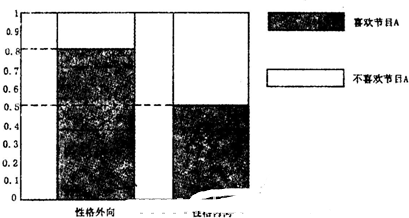
媒体为调查喜欢娱乐节目A是否与性格外向有关,随机抽取了500名性格外向的和500名性格内向的居民,抽查结果用等高条形图表示如下:
(1)作出2×2列联表;
(2)试用独立性检验的方法分析,能否在犯错的概率不超过0.001的前提下说明喜欢娱乐节目A与性格外向有关?

(1)作出2×2列联表;
(2)试用独立性检验的方法分析,能否在犯错的概率不超过0.001的前提下说明喜欢娱乐节目A与性格外向有关?
考点:独立性检验的应用
专题:计算题,概率与统计
分析:(1)由等高条形图可知,性格外向、性格内向的人中喜欢节目A的人数,可得2×2列联表;
(2)计算K2,与临界值比较,即可得出结论.
(2)计算K2,与临界值比较,即可得出结论.
解答:
解:(1)由等高条形图可知,性格外向的人中喜欢节目A的有500×0.8=400人,性格内向的人中喜欢节目A的有500×0.5=250人,
作2×2列联表如下
(2)K2=
≈98.901>10.828,
∴能在犯错的概率不超过0.001的前提下说明喜欢娱乐节目A与性格外向有关.
作2×2列联表如下
| 喜欢节目A | 喜欢节目B | 合计 | |
| 性格外向 | 400 | 100 | 500 |
| 性格内向 | 250 | 250 | 500 |
| 合计 | 650 | 350 | 1000 |
| 1000×(400×250-100×250)2 |
| 500×500×650×350 |
∴能在犯错的概率不超过0.001的前提下说明喜欢娱乐节目A与性格外向有关.
点评:本题考查独立性检验的应用,本题解题的关键是正确理解观测值对应的概率的意义.

练习册系列答案
相关题目
函数y=sin(2x-
)的一条对称轴为( )
| π |
| 6 |
A、x=-
| ||
B、x=
| ||
C、x=
| ||
D、x=-
|
已知数列{an}满足:am=
(am-1+am+1)(m>1,m∈N),a4=4,则a3+a4+a5=( )
| 1 |
| 2 |
| A、4 | B、8 | C、12 | D、16 |
在△ABC中,若a、b、c分别为角A、B、C所对的边,且cos2B+cosB+cos(A-C)=1,则有( )
| A、a、c、b 成等比数列 |
| B、a、c、b 成等差数列 |
| C、a、b、c 成等差数列 |
| D、a、b、c成等比数列 |
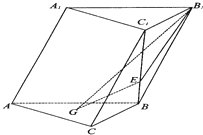 如图,在斜三棱柱ABC-A1B1C1中,侧面AA1B1B⊥底面ABC,侧棱AA1与底面ABC成60°的角,AA1=2.底面ABC是边长为2的正三角形,其重心为G点,E是线段BC1上一点,且BE=
如图,在斜三棱柱ABC-A1B1C1中,侧面AA1B1B⊥底面ABC,侧棱AA1与底面ABC成60°的角,AA1=2.底面ABC是边长为2的正三角形,其重心为G点,E是线段BC1上一点,且BE=