题目内容

设函数f（x）=sin（2ωx+
π
6
）+2sin2ωx（ω＞0），其图象的两个相邻对称中心的距离为
π
2
．
（1）求函数f（x）的解析式；
（2）若△ABC的内角为A，B，C，所对的边分别为a，b，c（其中b＜c），且f（A）=2，a=
7
，△ABC面积为
3
2
3
，求b，c的值．
考点：函数y=Asin（ωx+φ）的图象变换,三角函数中的恒等变换应用,余弦定理
专题：三角函数的图像与性质,解三角形
分析：（1）通过两角和与差的三角函数化简函数的表达式为一个角的一个三角函数的形式，图象的两个相邻对称中心的距离为
π
2
．求出函数的周期，然后求函数f（x）的解析式；
（2）利用解析式通过f（A）=2，求出A，通过a=
7
，△ABC面积为
3
2
3
，以及余弦定理即可求b，c的值．
解答： 解：（1）f(x)=sin(2ωx+
π
6
)+1-cos2ωx
=
3
2
sin2ωx-
1
2
cos2ωx+1
=sin(2ωx-
π
6
)+1…（3分）
由题意知T=π，∴
2π
2ω
=π，ω=1，
∴函数的解析式为：f(x)=sin(2x-
π
6
)+1…（6分）
（2）由f（A）=2，得sin(2A-
π
6
)=1，0＜A＜π，
∴A=
π
3
，
∴
3
3
2
=S△ABC=
1
2
bcsin
π
3
=
3
4
bc即bc=6，…（8分）
又a2=b2+c2-2bccosA，将a=
7
，A=
π
3
代入得b2+c2=13，…（10分）
又b＜c解
bc=6
b2+c2=13
得
b=2
c=3
…（12分）
点评：本题考查两角和与差的三角函数，函数的解析式的求法，余弦定理的应用，三角形的面积的求法，考查计算能力．
练习册系列答案
相关题目
在数列{an}中，若a1=-2，且对任意的n∈N*有2an+1=1+2an，则数列{an}前10项的和为（　　）
A、5
B、10
C、
5
2
D、
5
4
已知椭圆
x2
a2
+
y2
b2
=1（a＞b＞0）上的点 （
3
，
3
2
）到它的两个焦点的距离之和为4
（Ⅰ）求椭圆的方程：
（Ⅱ）A，B是椭圆上关于x轴对称的两点，设D（4，0），连接DB交椭圆于另一点F，证明直线AE恒过x轴上的定点P；
（Ⅲ）在（Ⅱ）的条件下，过点P的直线与椭圆交于M，N两点，求
OM
•
ON
的取值范围．
已知函数f（x）=ax2+ln（x+1）．
（1）当a=-
1
4
时，求函数f（x）的单调区间；
（2）当x∈[0，+∞）时，函数y=f（x）图象上的点都在
x≥0
y-x≤0
所表示的平面区域内，不等式f（x）≤x恒成立，求实数a的取值范围．
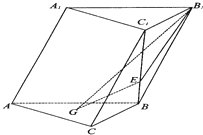如图，在斜三棱柱ABC-A1B1C1中，侧面AA1B1B⊥底面ABC，侧棱AA1与底面ABC成60°的角，AA1=2．底面ABC是边长为2的正三角形，其重心为G点，E是线段BC1上一点，且BE=
1
3
BC1．
（1）求证：GE∥侧面AA1B1B；
（2）求平面B1GE与底面ABC所成锐二面角的正切值；
（3）在直线AG上是否存在点T，使得B1T⊥AG？若存在，指出点T的位置；若不存在，说明理由．
已知数列{an}的首项a1=
3
5
，an+1=
3an
2an+1
，n=1，2，…
（1）求证：{
1
an
-1}是等比数列，并求出{an}的通项公式；
（2）证明：对任意的x＞0，an≥
1
1+x
-
1
(1+x)2
（
2
3n
-x），n=1，2，…
（3）证明：n-
2
5
≥a1+a2+…+an＞
n2
n+1
．
已知抛物线y2=2px（p＞0）的准线与x轴交于点M（-1，0）．
（Ⅰ）求抛物线的方程，并写出焦点坐标；
（Ⅱ）是否存在过焦点的直线AB（直线与抛物线交于点A，B），使得三角形MAB的面积S△MAB=4
2
？若存在，请求出直线AB的方程；若不存在，请说明理由．
已知向量
a
=（4，-3），向量
b
=（2，1），若
a
-t
b
与
b
的夹角为45°，求实数t的值．
执行如图的程序框图，若p=3，则输出的S=
 
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网