题目内容
已知z1,z2为复数,i为虚数单位,z1•
+3(z1+
)+5=0,
为纯虚数,z1,z2在复平面内对应的点分别为P,Q.
(1)求点P的轨迹方程;
(2)求点Q的轨迹方程;
(3)写出线段PQ长的取值范围.
. |
| z1 |
. |
| z1 |
| z2+3 |
| z2-3 |
(1)求点P的轨迹方程;
(2)求点Q的轨迹方程;
(3)写出线段PQ长的取值范围.
考点:轨迹方程
专题:直线与圆,数系的扩充和复数
分析:(1)设出复数z1=x+yi(x,y∈R),代入z1•
+3(z1+
)+5=0整理得到z1在复平面内对应的点P的轨迹方程;
(2)设z2=x+yi(x,y∈R),代入
,由其为纯虚数整理得到z2在复平面内对应的点Q的轨迹;
(3)画出P,Q的轨迹所表示的图形,数形结合求得线段PQ长的取值范围.
. |
| z1 |
. |
| z1 |
(2)设z2=x+yi(x,y∈R),代入
| z2+3 |
| z2-3 |
(3)画出P,Q的轨迹所表示的图形,数形结合求得线段PQ长的取值范围.
解答:
解:(1)设z1=x+yi(x,y∈R),
由z1•
+3(z1+
)+5=0,得:
(x+yi)(x-yi)+3(x+yi+x-yi)+5=0,
整理得(x+3)2+y2=4.
∴点P的轨迹方程为(x+3)2+y2=4;
(2)设z2=x+yi(x,y∈R),
=
=
,
∵
为纯虚数,
∴x2+y2=9且y≠0,
∴点Q的轨迹方程为x2+y2=9 (y≠0);
(3)如图,

由图可知,线段PQ长的取值范围[0,8].
由z1•
. |
| z1 |
. |
| z1 |
(x+yi)(x-yi)+3(x+yi+x-yi)+5=0,
整理得(x+3)2+y2=4.
∴点P的轨迹方程为(x+3)2+y2=4;
(2)设z2=x+yi(x,y∈R),
| z2+3 |
| z2-3 |
| x+3+yi |
| x-3+yi |
| x2+y2-9-6yi |
| (x-3)2+y2 |
∵
| z2+3 |
| z2-3 |
∴x2+y2=9且y≠0,
∴点Q的轨迹方程为x2+y2=9 (y≠0);
(3)如图,

由图可知,线段PQ长的取值范围[0,8].
点评:本题考查了轨迹方程,考查了复数的代数表示法及其几何意义,体现了数形结合的解题思想方法,是中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
设f(x)是定义在R上的偶函数,且在(-∞,0)上是增函数,设a=f(log47),b=f(log
3),c=f(2
),则a,b,c的大小关系是( )
| 1 |
| 2 |
| 2 |
| A、c<a<b |
| B、c<b<a |
| C、b<c<a |
| D、a<b<c |
在△ABC中,若a、b、c分别为角A、B、C所对的边,且cos2B+cosB+cos(A-C)=1,则有( )
| A、a、c、b 成等比数列 |
| B、a、c、b 成等差数列 |
| C、a、b、c 成等差数列 |
| D、a、b、c成等比数列 |
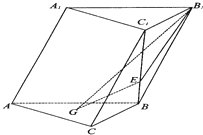 如图,在斜三棱柱ABC-A1B1C1中,侧面AA1B1B⊥底面ABC,侧棱AA1与底面ABC成60°的角,AA1=2.底面ABC是边长为2的正三角形,其重心为G点,E是线段BC1上一点,且BE=
如图,在斜三棱柱ABC-A1B1C1中,侧面AA1B1B⊥底面ABC,侧棱AA1与底面ABC成60°的角,AA1=2.底面ABC是边长为2的正三角形,其重心为G点,E是线段BC1上一点,且BE=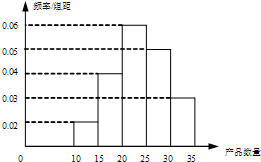 为了调查某厂2000名工人生产某种产品的能力,随机抽查了m位工人某天生产该产品的数量,产品数量的分组区间为[10,15),[15,20),[20,25),[25,30),[30,35],频率分布直方图如图所示.已知生产的产品数量在[20,25)之间的工人有6位,则m=
为了调查某厂2000名工人生产某种产品的能力,随机抽查了m位工人某天生产该产品的数量,产品数量的分组区间为[10,15),[15,20),[20,25),[25,30),[30,35],频率分布直方图如图所示.已知生产的产品数量在[20,25)之间的工人有6位,则m=